用python实现各种排序算法[python高级教程]
![用 python 实现各种排序算法[python高级教程]](/wp-content/uploads/new2022/20220602jjjkkk3/691225340_1.jpg)
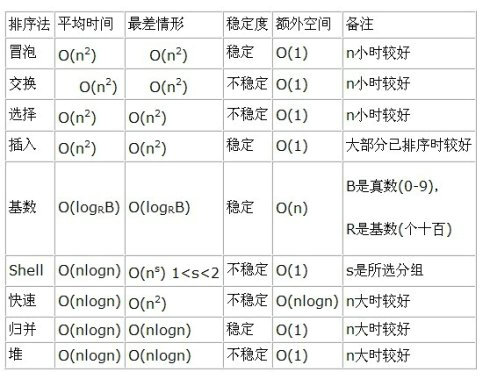
总结了一下常见集中排序的算法
归并排序
归并排序也称合并排序,是分治法的典型应用。分治思想是将每个问题分解成个个小问题,将每个小问题解决,然后合并。
具体的归并排序就是,将一组无序数按n/2递归分解成只有一个元素的子项,一个元素就是已经排好序的了。然后将这些有序的子元素进行合并。
合并的过程就是 对 两个已经排好序的子序列,先选取两个子序列中最小的元素进行比较,选取两个元素中最小的那个子序列并将其从子序列中
去掉添加到最终的结果集中,直到两个子序列归并完成。
代码如下:
#!/usr/bin/pythonimport sys
def merge(nums, first, middle, last):
''''' merge '''
# 切片边界,左闭右开并且是了0为开始
lnums = nums[first:middle+1]
rnums = nums[middle+1:last+1]
lnums.append(sys.maxint)
rnums.append(sys.maxint)
l = 0
r = 0
for i in range(first, last+1):
if lnums[l] < rnums[r]:
nums[i] = lnums[l]
l+=1
else:
nums[i] = rnums[r]
r+=1
def merge_sort(nums, first, last):
''''' merge sort
merge_sort函数中传递的是下标,不是元素个数
'''
if first < last:
middle = (first + last)/2
merge_sort(nums, first, middle)
merge_sort(nums, middle+1, last)
merge(nums, first, middle,last)
if __name__ == '__main__':
nums = [10,8,4,-1,2,6,7,3]
print 'nums is:', nums
merge_sort(nums, 0, 7)
print 'merge sort:', nums
稳定,时间复杂度 O(nlog n)
插入排序
代码如下:
python;toolbar:false">#!/usr/bin/pythonimport sys
def insert_sort(a):
''''' 插入排序
有一个已经有序的数据序列,要求在这个已经排好的数据序列中插入一个数,
但要求插入后此数据序列仍然有序。刚开始 一个元素显然有序,然后插入一
个元素到适当位置,然后再插入第三个元素,依次类推
'''
a_len = len(a)
if a_len = 0 and a[j] > key:
a[j+1] = a[j]
j-=1
a[j+1] = key
return a
if __name__ == '__main__':
nums = [10,8,4,-1,2,6,7,3]
print 'nums is:', nums
insert_sort(nums)
print 'insert sort:', nums
稳定,时间复杂度 O(n^2)
交换两个元素的值python中你可以这么写:a, b = b, a,其实这是因为赋值符号的左右两边都是元组
(这里需要强调的是,在python中,元组其实是由逗号“,”来界定的,而不是括号)。
选择排序
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小(大)元素,存放到
排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所
有元素均排序完毕。
import sysdef select_sort(a):
''''' 选择排序
每一趟从待排序的数据元素中选出最小(或最大)的一个元素,
顺序放在已排好序的数列的最后,直到全部待排序的数据元素排完。
选择排序是不稳定的排序方法。
'''
a_len=len(a)
for i in range(a_len):#在0-n-1上依次选择相应大小的元素
min_index = i#记录最小元素的下标
for j in range(i+1, a_len):#查找最小值
if(a[j]<a[min_index]):
min_index=j
if min_index != i:#找到最小元素进行交换
a[i],a[min_index] = a[min_index],a[i]
if __name__ == '__main__':
A = [10, -3, 5, 7, 1, 3, 7]
print 'Before sort:',A
select_sort(A)
print 'After sort:',A
不稳定,时间复杂度 O(n^2)
希尔排序
希尔排序,也称递减增量排序算法,希尔排序是非稳定排序算法。该方法又称缩小增量排序,因DL.Shell于1959年提出而得名。
先取一个小于n的整数d1作为第一个增量,把文件的全部记录分成d1个组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行排序;
然后,取第二个增量d2<d1重复上述的分组和排序,直至所取的增量dt=1(dt<dt-l<…<d2<d1),即所有记录放在同一组中进行直接插入排序为止。
import sysdef shell_sort(a):
''''' shell排序
'''
a_len=len(a)
gap=a_len/2#增量
while gap>0:
for i in range(a_len):#对同一个组进行选择排序
m=i
j=i+1
while j<a_len:
if a[j]<a[m]:
m=j
j+=gap#j增加gap
if m!=i:
a[m],a[i]=a[i],a[m]
gap/=2
if __name__ == '__main__':
A = [10, -3, 5, 7, 1, 3, 7]
print 'Before sort:',A
shell_sort(A)
print 'After sort:',A
不稳定,时间复杂度 平均时间 O(nlogn) 最差时间O(n^s)1<s<2
堆排序 ( Heap Sort )
"堆”的定义:在起始索引为 0 的“堆”中:
节点 i 的右子节点在位置 2 * i + 24) 节点 i 的父节点在位置 floor( (i - 1) / 2 ) : 注 floor 表示“取整”操作
堆的特性:
每个节点的键值一定总是大于(或小于)它的父节点
“最大堆”:
“堆”的根节点保存的是键值最大的节点。即“堆”中每个节点的键值都总是大于它的子节点。
上移,下移 :
当某节点的键值大于它的父节点时,这时我们就要进行“上移”操作,即我们把该节点移动到它的父节点的位置,
而让它的父节点到它的位置上,然后我们继续判断该节点,直到该节点不再大于它的父节点为止才停止“上移”。
现在我们再来了解一下“下移”操作。当我们把某节点的键值改小了之后,我们就要对其进行“下移”操作。
方法:
我们首先建立一个最大堆(时间复杂度O(n)),然后每次我们只需要把根节点与最后一个位置的节点交换,然后把最后一个位置排除之外,然后把交换后根节点的堆进行调整(时间复杂度 O(lgn) ),即对根节点进行“下移”操作即可。 堆排序的总的时间复杂度为O(nlgn).
代码如下:
#!/usr/bin env python
# 数组编号从 0开始
def left(i):
return 2*i +1
def right(i):
return 2*i+2
#保持最大堆性质 使以i为根的子树成为最大堆
def max_heapify(A, i, heap_size):
if heap_size <= 0:
return
l = left(i)
r = right(i)
largest = i # 选出子节点中较大的节点
if l A[largest]:
largest = l
if r A[largest]:
largest = r
if i != largest :#说明当前节点不是最大的,下移
A[i], A[largest] = A[largest], A[i] #交换
max_heapify(A, largest, heap_size)#继续追踪下移的点
#print A
# 建堆
def bulid_max_heap(A):
heap_size = len(A)
if heap_size >1:
node = heap_size/2 -1
while node >= 0:
max_heapify(A, node, heap_size)
node -=1
# 堆排序 下标从0开始
def heap_sort(A):
bulid_max_heap(A)
heap_size = len(A)
i = heap_size - 1
while i > 0 :
A[0],A[i] = A[i], A[0] # 堆中的最大值存入数组适当的位置,并且进行交换
heap_size -=1 # heap 大小 递减 1
i -= 1 # 存放堆中最大值的下标递减 1
max_heapify(A, 0, heap_size)
if __name__ == '__main__' :
A = [10, -3, 5, 7, 1, 3, 7]
print 'Before sort:',A
heap_sort(A)
print 'After sort:',A
不稳定,时间复杂度 O(nlog n)
快速排序
快速排序算法和合并排序算法一样,也是基于分治模式。对子数组A[p...r]快速排序的分治过程的三个步骤为:
分解:把数组A[p...r]分为A[p...q-1]与A[q+1...r]两部分,其中A[p...q-1]中的每个元素都小于等于A[q]而A[q+1...r]中的每个元素都大于等于A[q];
解决:通过递归调用快速排序,对子数组A[p...q-1]和A[q+1...r]进行排序;
合并:因为两个子数组是就地排序的,所以不需要额外的操作。
对于划分partition 每一轮迭代的开始,x=A[r], 对于任何数组下标k,有:
1) 如果p≤k≤i,则A[k]≤x。
2) 如果i+1≤k≤j-1,则A[k]>x。
3) 如果k=r,则A[k]=x。
代码如下:
#!/usr/bin/env python# 快速排序
'''''
划分 使满足 以A[r]为基准对数组进行一个划分,比A[r]小的放在左边,
比A[r]大的放在右边
快速排序的分治partition过程有两种方法,
一种是上面所述的两个指针索引一前一后逐步向后扫描的方法,
另一种方法是两个指针从首位向中间扫描的方法。
'''
#p,r 是数组A的下标
def partition1(A, p ,r):
'''''
方法一,两个指针索引一前一后逐步向后扫描的方法
'''
x = A[r]
i = p-1
j = p
while j < r:
if A[j] < x:
i +=1
A[i], A[j] = A[j], A[i]
j += 1
A[i+1], A[r] = A[r], A[i+1]
return i+1
def partition2(A, p, r):
'''''
两个指针从首尾向中间扫描的方法
'''
i = p
j = r
x = A[p]
while i = x and i < j:
j -=1
A[i] = A[j]
while A[i]<=x and i < j:
i +=1
A[j] = A[i]
A[i] = x
return i
# quick sort
def quick_sort(A, p, r):
'''''
快速排序的最差时间复杂度为O(n2),平时时间复杂度为O(nlgn)
'''
if p < r:
q = partition2(A, p, r)
quick_sort(A, p, q-1)
quick_sort(A, q+1, r)
if __name__ == '__main__':
A = [5,-4,6,3,7,11,1,2]
print 'Before sort:',A
quick_sort(A, 0, 7)
print 'After sort:',A
不稳定,时间复杂度 最理想 O(nlogn)最差时间O(n^2)
说下python中的序列:
列表、元组和字符串都是序列,但是序列是什么,它们为什么如此特别呢?序列的两个主要特点是索引操作符和切片操作符。索引操作符让我们可以从序列中抓取一个特定项目。切片操作符让我们能够获取序列的一个切片,即一部分序列,如:a = ['aa','bb','cc'], print a[0] 为索引操作,print a[0:2]为切片操作。
以上是 用python实现各种排序算法[python高级教程] 的全部内容, 来源链接: utcz.com/z/540171.html