【自考】数据结构第四章判定树和哈夫曼树,期末不挂科指南,第8篇
哈夫曼树">判定树和哈夫曼树
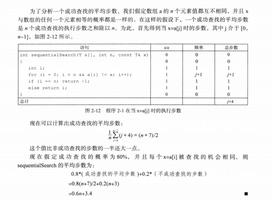
分类与判定树
这个小节有个比较重要的概念,就是用于描述分类过程的二叉树称为判定树 记住即可
哈夫曼树与哈夫曼算法
首先了解一下什么是哈夫曼树
给定一组值p~1~,...p~k~,如何构造一棵有k个叶子且分别以这些值为权的判定树,使得其平均比较次数最小。满足上述条件的判定树称为哈夫曼树。
哈夫曼率先给出了一个求哈夫曼树的简单而有效的方法,称为哈夫曼算法。
非形式的描述如下
- 给定的值{p~1~,p~2~,...,p~k~}构造森林{T~1~,T~2~,T~k~},其中每个T~i~为一棵只有根结点且其权为p~i~的二叉树。
- 从F中选取根结点的权最小的两棵二叉树T~i~和T~j~,构造一棵分别以T~i~和T~j~为左、右子树的新的二叉树T~h~,置T~h~根结点的权为T~i~,T~j~根结点的权值之和。
- 从F中删去T~i~和T~j~,并将T~h~加入F,若F中仍多于一棵二叉树,则返回第二步,直到F中只含有一棵二叉树为止,这棵树就是哈夫曼树。
参照案例
重点来了,看真题,请记住==哈夫曼树不唯一、时刻考虑权值最小==
真题参考
动态展示这道题目的解答方法,已经去掉了结点之间的连线
编码" title="哈夫曼编码">哈夫曼编码">哈夫曼编码
哈夫曼编码比较简单,就是将某棵二叉树中每个结点的左分支标志“0”,右分支标志“1”,这样,从根到每个叶结点形成“0”/“1”序列,将该序列作为叶结点对应字符的编码,由此得到的二进制编码称为哈夫曼编码。
请读题
设某通讯系统中一个待传输的文本有6个不同字符,它们的出现频率分别是0.5,0.8,1.4,2.2,2.3,2.8,试设计哈夫曼编码
教材中给出了树和哈夫曼编码,直接看一下即可
出现频率为0.5的字符编码为1000
出现频率为0.8的字符编码为1001
出现频率为1.4的字符编码为101
出现频率为2.2的字符编码为00
出现频率为2.3的字符编码为01
出现频率为2.8的字符编码为11
小结
树形结构的应用非常广泛,判定树和哈夫曼树可分别用于求解分类问题和有效分类问题以及哈夫曼编码,哈夫曼编码算法的关键点是:每次合并具有最小权值和次小权值的两个根结点,直到只剩下一个根结点为止。
对哈夫曼树的每个结点的左分支和右分支分别置“0”或“1”,就可得到哈夫曼编码。
以上是 【自考】数据结构第四章判定树和哈夫曼树,期末不挂科指南,第8篇 的全部内容, 来源链接: utcz.com/z/532003.html