最短路径算法(迪杰斯特拉)

迪杰斯特拉(Dijkstra)算法是求解“图”中单源路径" title="最短路径">最短路径的算法之一,所谓单源最短路径是指给定一个“初始节点”,求解其到其它各顶点的最短路径。
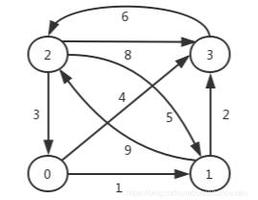
为了方便描述,假设图中所有边的权重都不为负:
该图已经较简洁,并且方便对该算法进行描述:
假设1号节点为指定的开始节点,现欲求1号节点到2、3、4号各节点的最短路径。其中1号到2号节点的求解过程如下:
(1)由于1号节点与2、3、4号节点直接相连的路径分别为w6、w5、w1(我们将这几个路径放到一个临时的集合中,并试图从中选择一个到其它节点中路径最短的那个)。
(2)如果临时集合中w6为其中的最短路径,则w6为最终结果,关键问题是w1 -> w4,w1 -> w3 -> w2,w5 -> w2,w5 -> w3 -> w4也是其余的4条路径。所以我们假设(1)中w1为与1号节点直连路径中最短的那条(因此w1为1号节点和4号节点的最短路径,我们将4号节点放入到最终的最短路径集合中)。
(3)对于4号节点,除了直连的1号节点外,还有其余的2号节点和3号节点。如果w1 -> w4的路径和小于w6,那么临时集合中1号与2号节点的最短路径需更新为w1+w4(假设更新)。同理w1 -> w3的路径和小于w5,则临时集合中1号与3号节点的最短路径需更新为w1+w3(假设更新,注意我们的目标是求1号到2号节点的最短路径,但是该算法会附带着求解到其它节点的最短路径)。
(4)目前为止在临时集合中保存着1号节点分别到2号节点和3号节点的最短路径,现按照(2)的步骤从其中选择一条最短路径来,如果选择2号节点则为最终结果,如果选择3号节点则需要按照(3)的步骤进一步判断如果w1 -> w3 -> w2的路径和小于w1 -> w4则最终的最短路径更新为w1+w3+w2。
注意:以上就是该算法的全过程,而且前提条件是权重不为负。那么假设权重可能为负则该算法的第(1)步就不能实现,因为一开始就不能选择一个到其它节点中路径最短的那个节点,这是前提条件。当然该算法在真正实现的时候还需要考虑一下权重相等的情况,具体代码请参考我给出的开源实现。
以上是 最短路径算法(迪杰斯特拉) 的全部内容, 来源链接: utcz.com/z/510404.html