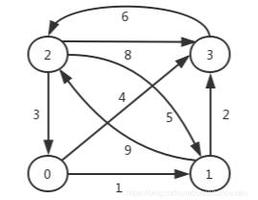
【算法】单元最短路径之BellmanFord算法和SPFA算法

SPFA是经过对列优化的bellman-Ford算法,因此,在学习SPFA算法之前,先学习下bellman-Ford算法。
bellman-Ford算法是一种通过松弛操作计算最短路的算法。
适用条件
1.单源最短路径(从源点s到其它所有顶点v);
2.有向图&无向图(无向图可以看作(u,v),(v,u)同属于边集E的有向图);
3.边权可正可负(如有负权回路输出错误提示);
4.差分约束系统;
bellman-Ford的具体操作是这样的:
- 初始化,dis数组表示从起点到达第i个点的最短距离。初始化时:dis[i]=edge[起点][i];如果没有边相接,则设为MAXN;
- 循环n-1次,遍历每个边,将dis[边[i].目标节点]=min(dis[边[i].目标节点],dis[边[i].初始节点]+边[i].权值);
- 【可选】检验负权回路:判断边集合中的每一条边的两个端点是否收敛。如果存在未收敛的顶点,则算法返回false,表明问题无解;否则算法返回true,并且从源点可达的顶点v的最短距离保存在 dis[v]中。
#include <bits/stdc++.h>usingnamespace std;
int n,m;
//Bellman-Ford algorithm
struct Edge
{
int a,b,v;
}edge[500005];
longlong dis[500005];
void bellman_ford(int x)
{
dis[x]=0;
for(int i=1;i<=n-1;i++)
{
for(int j=1;j<=m;j++)
{
dis[edge[j].b]=min(dis[edge[j].b],dis[edge[j].a]+edge[j].v);
}
}
return ;
/*
bool flag = 1; //判断是否含有负权回路
for(int i = 1; i <= m; ++i) if(dis[edge[i].b] > dis[edge[i].a] + edge[i].cost)
{
flag = 0;
break;
}
return flag;
*/
}
int main()
{
int s;
cin>>n>>m>>s;
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&edge[i].a,&edge[i].b,&edge[i].v);
}
for(int i=1;i<=n;i++)dis[i]=2147483647;
bellman_ford(s);
for(int i=1;i<=n;i++)
cout<<dis[i]<<"";
return0;
}
这个算法在luogu上70分,TLE了两个测试点,因此需要学习一个更牛逼的算法,SPFA,听说这是一个交大的教授发明的。附上原论文连接:https://wenku.baidu.com/view/df249954d4d8d15abe234eff.html
SPFA算法的全称是:Shortest Path Faster Algorithm,是西南交通大学段凡丁于 1994 年发表的论文中的名字。不过,段凡丁的证明是错误的,且在 Bellman-Ford 算法提出后不久(1957 年 )已有队列优化内容,所以国际上不承认 SPFA 算法是段凡丁提出的。
为了避免最坏情况的出现,在正权图上应使用效率更高的Dijkstra算法。若给定的图存在负权边,类似Dijkstra算法等算法便没有了用武之地,SPFA算法便派上用场了。
简洁起见,我们约定加权有向图G不存在负权回路,即最短路径一定存在。用数组d记录每个结点的最短路径估计值,而且用邻接表来存储图G。我们采取的方法是动态逼近法:设立一个先进先出的队列用来保存待优化的结点,优化时每次取出队首结点u,并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作,如果v点的最短路径估计值有所调整,且v点不在当前的队列中,就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作,直至队列空为止。
定理:只要最短路径存在,上述SPFA算法必定能求出最小值。证明:每次将点放入队尾,都是经过松弛操作达到的。换言之,每次的优化将会有某个点v的最短路径估计值d[v]变小。所以算法的执行会使d越来越小。由于我们假定图中不存在负权回路,所以每个结点都有最短路径值。因此,算法不会无限执行下去,随着d值的逐渐变小,直到到达最短路径值时,算法结束,这时的最短路径估计值就是对应结点的最短路径值。
#include <bits/stdc++.h>usingnamespace std;
int n,m,start;
longlong dis[1000005],used[1000005],head[1000005];
int num_edge=0;
struct Graph
{
int to,w,next;
}graph[10000005];
bool spfa(int x)
{
queue <int> q;
dis[x]=0;
used[x]=1;
q.push(x);
while(!q.empty())
{
int u=q.front();
q.pop();
used[u]=0;
for(int i=head[u];i;i=graph[i].next)
{
int v=graph[i].to;
longlong Songchi=dis[u]+graph[i].w;
if(dis[v]>Songchi)
{
dis[v]=Songchi;
if(used[v]==0)
{
used[v]=1;
q.push(v);
}
}
}
}
return1;
}
void addedge(intfrom,int to,int dis)//邻接表存边
{
graph[++num_edge].next=head[from];
graph[num_edge].to=to;
graph[num_edge].w=dis;
head[from]=num_edge;
}
int main()
{
memset(head,0,sizeof(head));
memset(used,0,sizeof(used));
cin>>n>>m>>start;
for(int i=1;i<=n;i++)dis[i]=2147483647;
for(int i=1;i<=m;i++)
{
int a,b,w;
scanf("%d%d%d",&a,&b,&w);
addedge(a,b,w);
}
if(spfa(start))
{
for(int i=1;i<=n;i++)
cout<<dis[i]<<"";
}
}
以上是 【算法】单元最短路径之BellmanFord算法和SPFA算法 的全部内容, 来源链接: utcz.com/z/509542.html