堆排序算法以及JAVA实现

  • Z时代
  • 2024-01-10
  • 分类：综合

java

堆的定义如下：

　　n个元素的序列{k0,k1,...,ki,…,k(n-1)}当且仅当满足下关系时，称之为堆。

　　" ki<=k2i,ki<=k2i+1;或ki>=k2i,ki>=k2i+1.（i=1,2,…,[n/2])"

　　若将和此次序列对应的一维数组（即以一维数组作此序列的存储结构）看成是一个完全二叉树，

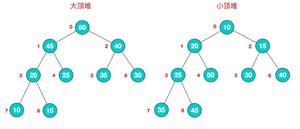
　　则完全二叉树中每一个节点的值的都大于或等于任意一个字节的值（如果有的话），称之为大顶堆。

　　则完全二叉树中每一个节点的值的都小于或等于任意一个字节的值（如果有的话），称之为小顶堆。

　　由此，若序列{k0,k1,…,k(n-1)}是堆，则堆顶元素（或完全二叉树的根）必为序列中n个元素的最小值（或最大值）。

　　倘若给堆中每一个节点都赋予一个整数值标签，根节点被标记为0，对于每一个标记为i的节点，其左子节点（若存在的话）被标记为2*i+1，其右子节点（若存在的话）被标记为2*i+2，对于一个标记为i的非根节点，其父节点被标记为（i-1）/2。使用这个标记，我们能够将堆存储在数组中，节点存储在数据中的位置就使其标签。

排序算法" title="堆排序算法">堆排序算法：

sort(A)
    buildHeap(A)
    for i=n-1 downto 1 do
        swap A[0] with A[i]
        heapify(A,0,i)
end
buildHeap(A)
    for i=n/2 - 1 downto 0 do
        heapify(A,i,n)
end
heapify(A,idx,max)
    left = 2*idx +1
    right = 2*idx +2
    if(left<max and A[left]>A[idx]) then
        largest = left
    else
        largest = idx
    if(right < max and A[right]>A[largest]) then
        largest = ritht
    if(largest!=idx) then
        swap A[largest] with A[idx]
        heapify(A,largest,max)
end

 堆排序的JAVA语言实现 ：

package org.myorg.algorithm;
public class HeapSorter {
    public static void heapSort(int[] array){
        buildHeap(array);//构建堆
        int n = array.length;
        int i=0;
        for(i=n-1;i>=1;i--){
            swap(array,0,i);
            heapify(array,0,i);
            }
    }
    public static void buildHeap(int[] array){
        int n = array.length;//数组中元素的个数
        for(int i=n/2-1;i>=0;i--)
            heapify(array,i,n);
    }
    public static void heapify(int[] A,int idx,int max){
        int left = 2*idx+1;// 左孩子的下标（如果存在的话）
        int right =2*idx+2;// 左孩子的下标（如果存在的话）
        int largest = 0;//寻找3个节点中最大值节点的下标
        if(left<max && A[left]>A[idx])
            largest = left;
        else
            largest = idx;
        if(right<max && A[right]>A[largest])
            largest = right;
        if(largest!=idx){
            swap(A,largest,idx);
            heapify(A,largest,max);            
            }    
    }
    public static void swap(int[] array,int i,int j){
        int temp =0;
        temp=array[i];
        array[i]=array[j];
        array[j]=temp;
    }
    public static void main(String[] args) {
        int[] a = {1,2,3,4,5,6,7,16,9,10,11,12,13,14,15,8};
        System.out.println("排序前..........................");
        for(int i=0;i<a.length;i++)
            System.out.println(a[i]);
        heapSort(a);
        System.out.println("排序后..........................");
        for(int i=0;i<a.length;i++)
            System.out.println(a[i]);
    }
}

以上是 堆排序算法以及JAVA实现 的全部内容， 来源链接： utcz.com/z/394677.html

回到顶部