java几种常见的排序算法总结

Z时代
2024-01-10
分类：综合

java

[java] view plain copy

/*************几种常见的排序算法总结***************************/

package paixu;

public class PaiXu {

final int MAX=20;

int num[]=new int[MAX];

{

System.out.print("生成的随机数组是：");

for(int i=0;i<20;i++){

num[i]=(int)(Math.random()*100);

System.out.print(num[i]+" ");

}

System.out.println();

}

int num2[]=new int[MAX]; //只用于合并排序法中

{

System.out.print("合并排序法需要使用的数组2是：");

for(int i=0;i<20;i++){

num2[i]=(int)(Math.random()*100);

System.out.print(num2[i]+" ");

}

System.out.println();

}

int num3[]=new int[MAX+MAX]; //用于存放合并排序法中被合并排序好的数组

public PaiXu(){

selsort(num.clone()); //选择排序法

insort(num.clone()); //插入排序法

bubsort(num.clone()); //冒泡排序法

shellsort(num.clone()); //希尔排序法

shakersort(num.clone()); //shake排序法

heapsort(num.clone()); //堆排序

quicksort_one(num.clone()); //快速排序法（一）

quicksort_two(num.clone()); //快速排序法（二）

quicksort_three(num.clone()); //快速排序法（三）

mergesort(num.clone(),num2.clone(),num3); //合并排序法

basesort(num.clone()); //基数排序法

}

/*----------------------------选择排序法-------------------------------------------

将要排序的对象分作两部份，一个是已排序的，一个是未排序的，从后端未排序部份选择一个最小值，并放入前端已排序部份的最后一个。

-------------------------------------------------------------------------------*/

public void selsort(int number[]) {

int i, j, k, m, temp;

long start,end;

start=System.nanoTime();

for(i = 0; i < MAX-1; i++) {

m = i;

for(j = i+1; j < MAX; j++){

if(number[j] < number[m]){

m = j;

}

}

if( i != m){

temp=number[i];

number[i]=number[m];

number[m]=temp;

}

}

end=System.nanoTime();

System.out.println("-----------------选择排序法------------------");

System.out.print("排序后是:");

for(i=0;i<=MAX-1;i++){

System.out.print(number[i]+" ");

}

System.out.println();

System.out.println("排序使用时间："+(end-start)+" ns");

}

/*-------------------------插入排序法--------------------------------

像是玩朴克一样，我们将牌分作两堆，每次从后面一堆的牌抽出最前端的牌，然后插入前面一堆牌的适当位置

-----------------------------------------------------------------*/

public void insort(int number[]){

int i, j, k, temp;

long start,end;

start=System.nanoTime();

for(j = 1; j < MAX; j++) {

temp = number[j];

i = j - 1;

while(temp < number[i]) {

number[i+1] = number[i];

i--;

if(i == -1){

break;

}

}

number[i+1] = temp;

}

end=System.nanoTime();

System.out.println("-----------------插入排序法------------------");

System.out.print("排序后是:");

for(i=0;i<=MAX-1;i++){

System.out.print(number[i]+" ");

}

System.out.println();

System.out.println("排序使用时间："+(end-start)+" ns");

}

/*-----------------------------------------冒泡排序法----------------------------------------

顾名思义，就是排序时，最大的元素会如同气泡一样移至右端，其利用比较相邻元素的方法，将大的元素交换至右端，

所以大的元素会不断的往右移动，直到适当的位置为止。

基本的气泡排序法可以利用旗标的方式稍微减少一些比较的时间，当寻访完阵列后都没有发生任何的交换动作，

表示排序已经完成，而无需再进行之后的回圈比较与交换动作。

----------------------------------------------------------------------------------------*/

public void bubsort(int number[]){

int i, j, k, temp, flag = 1;

long start,end;

start=System.nanoTime();

for(i = 0; i < MAX-1 && flag == 1; i++) {

flag = 0;

for(j = 0; j < MAX-i-1; j++) {

if(number[j+1] < number[j]) {

temp=number[j+1];

number[j+1]=number[j];

number[j]=temp;

flag = 1;

}

}

}

end=System.nanoTime();

System.out.println("-----------------冒泡排序法------------------");

System.out.print("排序后是:");

for(i=0;i<=MAX-1;i++){

System.out.print(number[i]+" ");

}

System.out.println();

System.out.println("排序使用时间："+(end-start)+" ns");

}

/*--------------------------shell（希尔）排序法----------------------------

Shell首先将间隔设定为n/2，然后跳跃进行插入排序，再来将间隔n/4，跳跃进行排序动作，再来

间隔设定为n/8、n/16，直到间隔为1之后的最后一次排序终止，由于上一次的排序动作都会将

固定间隔内的元素排序好，所以当间隔越来越小时，某些元素位于正确位置的机率越高，因此

最后几次的排序动作将可以大幅减低。

---------------------------------------------------------------------*/

public void shellsort(int number[]) {

int i, j, k, gap, temp;

long start,end;

start=System.nanoTime();

gap = MAX / 2;

while(gap > 0) {

for(k = 0; k < gap; k++) {

for(i = k+gap; i < MAX; i+=gap) {

for(j = i - gap; j >= k; j-=gap) {

if(number[j] > number[j+gap]) {

temp=number[j];

number[j]=number[j+gap];

number[j+gap]=temp;

}else{

break;

}

}

}

}

gap /= 2;

}

end=System.nanoTime();

System.out.println("-----------------shell(希尔)排序法（改进的插入排序法）------------------");

System.out.print("排序后是:");

for(i=0;i<=MAX-1;i++){

System.out.print(number[i]+" ");

}

System.out.println();

System.out.println("排序使用时间："+(end-start)+" ns");

}

/*---------------------Shake排序法（改良的冒泡排序法）--------------------------

方法就在于气泡排序的双向进行，先让气泡排序由左向右进行，再来让气泡排序由右往左进行，

如此完成一次排序的动作，而您必须使用left与right两个旗标来记录左右两端已排序的元素位置。

--------------------------------------------------------------------*/

public void shakersort(int number[]) {

int i, temp, left = 0, right = MAX - 1, shift = 0;

long start,end;

start=System.nanoTime();

while(left < right) {

// 向右進行氣泡排序

for(i = left; i < right; i++) {

if(number[i] > number[i+1]) {

temp=number[i];

number[i]=number[i+1];

number[i+1]=temp;

shift = i;

}

}

right = shift;

// 向左進行氣泡排序

for(i = right; i > left; i--) {

if(number[i] < number[i-1]) {

temp=number[i];

number[i]=number[i-1];

number[i-1]=temp;

shift = i;

}

}

left = shift;

}

end=System.nanoTime();

System.out.println("-----------------shake排序法（改进的冒泡排序法）------------------");

System.out.print("排序后是:");

for(i=0;i<=MAX-1;i++){

System.out.print(number[i]+" ");

}

System.out.println();

System.out.println("排序使用时间："+(end-start)+" ns");

}

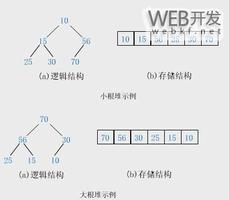
/*-----------------------heap排序（堆排序法--改进的选择排序）----------------------------

利用堆积树的原理，先构造一个堆积树（看堆积树的定义，笔记本上有），然后将根节点与最后的叶子节点交换，并屏蔽掉最后一个叶子节点，

然后再将未被屏蔽的部分重新构造堆积树，然后再重复上面的步骤，直到所有的数被按顺序排好。

--------------------------------------------------------------------------------*/

public void heapsort(int number[]) {

int i, m, p, s, temp;

long start,end;

start=System.nanoTime();

int number_temp[]=new int[MAX+1];

for(int temp_i=1;temp_i<MAX+1;temp_i++){

number_temp[temp_i]=number[temp_i-1];

}

createheap(number_temp);

m = MAX;

while(m > 1) {

temp=number_temp[1];

number_temp[1]=number_temp[m];

number_temp[m]=temp;

m--;

p = 1;

s = 2 * p;

while(s <= m) {

if(s < m && number_temp[s+1] > number_temp[s])

s++;

if(number_temp[p] >= number_temp[s])

break;

temp=number_temp[p];

number_temp[p]=number_temp[s];

number_temp[s]=temp;

p = s;

s = 2 * p;

}

}

for(int temp_j=1;temp_j<MAX+1;temp_j++){

number[temp_j-1]=number_temp[temp_j];

}

end=System.nanoTime();

System.out.println("-----------------heap排序（堆排序法--改进的选择排序）------------------");

System.out.print("排序后是:");

for(i=0;i<=MAX-1;i++){

System.out.print(number[i]+" ");

}

System.out.println();

System.out.println("排序使用时间："+(end-start)+" ns");

}

//将原数组构造为从下标1开始的一个新数组，便于处理，同时将这个新数组构造为最初始的堆积树结构

public void createheap(int number[]) {

int i, s, p, temp;

int heap[] = new int[MAX+1];

for(i = 1; i <= MAX; i++) {

heap[i] = number[i];

s = i;

p = i / 2;

while(s >= 2 && heap[p] < heap[s]) {

temp=heap[p];

heap[p]=heap[s];

heap[s]=temp;

s = p;

p = s / 2;

}

}

for(i = 1; i <= MAX; i++){

number[i] = heap[i];

}

}

/*-----------------------快速排序法（一）---------------------------------------------

这边所介绍的快速演算如下：将最左边的数设定为轴，并记录其值为s

廻圈处理：

令索引i 从数列左方往右方找，直到找到大于s 的数

令索引j 从数列左右方往左方找，直到找到小于s 的数

如果i >= j，则离开回圈

如果i < j，则交换索引i与j两处的值

将左侧的轴与j 进行交换

对轴左边进行递回

对轴右边进行递回

--------------------------------------------------------------------------------*/

public void quicksort_one(int number[]){

long start,end;

start=System.nanoTime();

quicksort_1(number,0,MAX-1);

end=System.nanoTime();

System.out.println("-----------------快速排序法（一）------------------");

System.out.print("排序后是:");

for(int i=0;i<=MAX-1;i++){

System.out.print(number[i]+" ");

}

System.out.println();

System.out.println("排序使用时间："+(end-start)+" ns");

}

public void quicksort_1(int number[],int left,int right) {

int i, j, s, temp;

if(left < right) {

s = number[left];

i = left;

j = right + 1;

while(true) {

// 向右找

while(i + 1 < number.length && number[++i] < s) ;

// 向左找

while(j -1 > -1 && number[--j] > s) ;

if(i >= j)

break;

temp=number[i];

number[i]=number[j];

number[j]=temp;

}

number[left] = number[j];

number[j] = s;

quicksort_1(number, left, j-1); // 对左边进行递回

quicksort_1(number, j+1, right); // 对右边进行递回

}

}

/*-----------------------快速排序法（二）---------------------------------------------

在这个例子中，取中间的元素s作比较，同样的先得右找比s大的索引i，然后找比s小的

索引j，只要两边的索引还没有交会，就交换i 与j 的元素值，这次不用再进行轴的交换了，

因为在寻找交换的过程中，轴位置的元素也会参与交换的动作，例如：

41 24 76 11 45 64 21 69 19 36

首先left为0，right为9，(left+right)/2 = 4（取整数的商），所以轴为索引4的位置，比较的元素是

45，您往右找比45大的，往左找比45小的进行交换：

41 24 76* 11 [45] 64 21 69 19 *36

41 24 36 11 45* 64 21 69 19* 76

41 24 36 11 19 64* 21* 69 45 76

[41 24 36 11 19 21] [64 69 45 76]

完成以上之后，再初别对左边括号与右边括号的部份进行递回，如此就可以完成排序的目的。

--------------------------------------------------------------------------------*/

public void quicksort_two(int number[]){

long start,end;

start=System.nanoTime();

quicksort_2(number,0,MAX-1);

end=System.nanoTime();

System.out.println("-----------------快速排序法（二）------------------");

System.out.print("排序后是:");

for(int i=0;i<=MAX-1;i++){

System.out.print(number[i]+" ");

}

System.out.println();

System.out.println("排序使用时间："+(end-start)+" ns");

}

public void quicksort_2(int number[], int left, int right) {

int i, j, s, temp;

if(left < right) {

s = number[(left+right)/2];

i = left - 1;

j = right + 1;

while(true) {

while(number[++i] < s) ; // 向右找

while(number[--j] > s) ; // 向左找

if(i >= j)

break;

temp=number[i];

number[i]=number[j];

number[j]=temp;

}

quicksort_2(number, left, i-1); // 对左边进行递回

quicksort_2(number, j+1, right); // 对右边进行递回

}

}

/*-----------------------快速排序法（三）---------------------------------------------

先说明这个快速排序法的概念，它以最右边的值s作比较的标准，将整个数列分为三个部份，

一个是小于s的部份，一个是大于s的部份，一个是未处理的部份，如下所示：

i j

--------|-----------|----------|s

小于s 大于s 未处理

在排序的过程中，i 与j 都会不断的往右进行比较与交换，最后数列会变为以下的状态：

-------------|-----------------|s

小于s 大于s

然后将s的值置于中间，接下来就以相同的步骤会左右两边的数列进行排序的动作，如下所示：

-------------|s|---------------

小于s 大于s

然后采用递归的方法重复上面的步骤，就可以实现排序了。

--------------------------------------------------------------------------------*/

public void quicksort_three(int number[]){

long start,end;

start=System.nanoTime();

quicksort_3(number,0,MAX-1);

end=System.nanoTime();

System.out.println("-----------------快速排序法（三）------------------");

System.out.print("排序后是:");

for(int i=0;i<=MAX-1;i++){

System.out.print(number[i]+" ");

}

System.out.println();

System.out.println("排序使用时间："+(end-start)+" ns");

}

public int partition(int number[], int left, int right) {

int i, j, s, temp;

s = number[right];

i = left - 1;

for(j = left; j < right; j++) {

if(number[j] <= s) {

i++;

temp=number[i];

number[i]=number[j];

number[j]=temp;

}

}

temp=number[i+1];

number[i+1]=number[right];

number[right]=temp;

return i+1;

}

public void quicksort_3(int number[], int left, int right) {

int q;

if(left < right) {

q = partition(number, left, right);

quicksort_3(number, left, q-1);

quicksort_3(number, q+1, right);

}

}

/*-----------------------合并排序法---------------------------------------------

合并排序法基本是将两笔已排序的资料合并并进行排序，如果所读入的资料尚未排序，

可以先利用其它的排序方式来处理这两笔资料，然后再将排序好的这两笔资料合并。

合并排序法中用到了快速排序法（三）

--------------------------------------------------------------------------------*/

public void mergesort(int number1[],int number2[],int number3[]){

long start,end;

start=System.nanoTime();

quicksort_3(number1,0,MAX-1);

quicksort_3(number2,0,MAX-1);

mergesort_merge(number1,MAX,number2,MAX,number3);

end=System.nanoTime();

System.out.println("-----------------合并排序法------------------");

System.out.print("排序后是:");

for(int i=0;i<=MAX+MAX-1;i++){

System.out.print(number3[i]+" ");

}

System.out.println();

System.out.println("排序使用时间："+(end-start)+" ns");

}

public void mergesort_merge(int number1[], int M, int number2[], int N, int number3[]) {

int i = 0, j = 0, k = 0;

while(i < M && j < N) {

if(number1[i] <= number2[j]){

number3[k++] = number1[i++];

}else{

number3[k++] = number2[j++];

}

}

while(i < M){

number3[k++] = number1[i++];

}

while(j < N){

number3[k++] = number2[j++];

}

}

/*-----------------------基数排序法---------------------------------------------

基数排序的方式可以采用LSD（Least sgnificant digital）或MSD（Most sgnificant digital），

LSD的排序方式由键值的最右边开始，而MSD则相反，由键值的最左边开始。

以LSD为例，假设原来有一串数值如下所示：

73, 22, 93, 43, 55, 14, 28, 65, 39, 81

首先根据个位数的数值，在走访数值时将它们分配至编号0到9的桶子中：

0 1 2 3 4 5 6 7 8 9

81 65 39

43 14 55 28

93

22 73

接下来将这些桶子中的数值重新串接起来，成为以下的数列：

81, 22, 73, 93, 43, 14, 55, 65, 28, 39

接着再进行一次分配，这次是根据十位数来分配：

接下来将这些桶子中的数值重新串接起来，成为以下的数列：

0 1 2 3 4 5 6 7 8 9

28 39

14 22 43 55 65 73 81 93

14, 22, 28, 39, 43, 55, 65, 73, 81, 93

这时候整个数列已经排序完毕；如果排序的对象有三位数以上，则持续进行以上的动作直至最

高位数为止。

LSD的基数排序适用于位数小的数列，如果位数多的话，使用MSD的效率会比较好，MSD的方

式恰与LSD相反，是由高位数为基底开始进行分配，其他的演算方式则都相同。

--------------------------------------------------------------------------------*/

public void basesort(int number[]){

int temp[][] = new int[MAX][MAX];

int order[] = new int[MAX];

int i, j, k, n, lsd;

long start,end;

k = 0;

n = 1;

start=System.nanoTime();

while(n <= 10) {

for(i = 0; i < MAX; i++) {

lsd = ((number[i] / n) % 10);

temp[lsd][order[lsd]] = number[i];

order[lsd]++;

}

//重新排列

for(i = 0; i < MAX; i++) {

if(order[i] != 0)

for(j = 0; j < order[i]; j++) {

number[k] = temp[i][j];

k++;

}

order[i] = 0;

}

n *= 10;

k = 0;

}

end=System.nanoTime();

System.out.println("-----------------基数排序法------------------");

System.out.print("排序后是:");

for(int ii=0;ii<=MAX-1;ii++){

System.out.print(number[ii]+" ");

}

System.out.println();

System.out.println("排序使用时间："+(end-start)+" ns");

}

public static void main(String[] args){

System.out.println("以下的测试时间仅供参考...");

new PaiXu();

}

}

以上代码的运行结果如下所示：

[plain] view plain copy

以下的测试时间仅供参考...

生成的随机数组是：53 82 61 70 75 31 30 68 22 56 48 23 12 74 13 85 69 62 21 55

合并排序法需要使用的数组2是：2 12 48 18 93 13 98 87 55 77 89 56 6 31 56 38 59 76 90 30

-----------------选择排序法------------------

排序后是:12 13 21 22 23 30 31 48 53 55 56 61 62 68 69 70 74 75 82 85

排序使用时间：7815 ns

-----------------插入排序法------------------

排序后是:12 13 21 22 23 30 31 48 53 55 56 61 62 68 69 70 74 75 82 85

排序使用时间：7475 ns

-----------------冒泡排序法------------------

排序后是:12 13 21 22 23 30 31 48 53 55 56 61 62 68 69 70 74 75 82 85

排序使用时间：18008 ns

-----------------shell(希尔)排序法（改进的插入排序法）------------------

排序后是:12 13 21 22 23 30 31 48 53 55 56 61 62 68 69 70 74 75 82 85

排序使用时间：11212 ns

-----------------shake排序法（改进的冒泡排序法）------------------

排序后是:12 13 21 22 23 30 31 48 53 55 56 61 62 68 69 70 74 75 82 85

排序使用时间：14610 ns

-----------------heap排序（堆排序法--改进的选择排序）------------------

排序后是:12 13 21 22 23 30 31 48 53 55 56 61 62 68 69 70 74 75 82 85

排序使用时间：15969 ns

-----------------快速排序法（一）------------------

排序后是:12 13 21 22 23 30 31 48 53 55 56 61 62 68 69 70 74 75 82 85

排序使用时间：8834 ns

-----------------快速排序法（二）------------------

排序后是:12 13 21 22 23 30 31 48 53 55 56 61 62 68 69 70 74 75 82 85

排序使用时间：9853 ns

-----------------快速排序法（三）------------------

排序后是:12 13 21 22 23 30 31 48 53 55 56 61 62 68 69 70 74 75 82 85

排序使用时间：10533 ns

-----------------合并排序法------------------

排序后是:2 6 12 12 13 13 18 21 22 23 30 30 31 31 38 48 48 53 55 55 56 56 56 59 61 62 68 69 70 74 75 76 77 82 85 87 89 90 93 98

排序使用时间：20387 ns

-----------------基数排序法------------------

排序后是:12 13 21 22 23 30 31 48 53 55 56 61 62 68 69 70 74 75 82 85

排序使用时间：8495 ns

以上是 java几种常见的排序算法总结的全部内容，来源链接： utcz.com/z/392279.html

回到顶部