红黑树与数据结构在Java集合中的应用

目录
- 一、数据类型
- 1. 数组
- 2. 链表
- 3. 树
- 3.1 红黑树
- 二、集合
- 2.1 List集合
- 1. ArrayList
- new ArrayList(?)初始操作
- add()
- get()
- set()
- remove()
- FailFast机制
- 2. LinkedList
- push(),add()
- get()
- set()
- 3. Vector(已过时)
- Vector子类Stack
- 怎么让集合线程安全
- 1. ArrayList
- 2.2 Set集合
- 1. HashSet简单介绍
- 概述
- add()
- 特点
- 2. TreeSet
- 概述
- add()
- 1. HashSet简单介绍
- 2.3 Map集合
- 1. Map集合的特点
- 2. TreeMap
- put()
- 3. HashMap
- HashMap简单介绍
- put()
- 2.1 List集合
一、数据类型
1. 数组
Char[] cs = new Char[] {\'G\', \'P\'};Char[] cs = new Char[2];
cs[0] = \'G\';
cs[1] = \'P\';
特点:
- 内存地址连续,使用之前必须要指定数组长度,先分配连续的内存空间,多长的一个地址
- 可以通过下标的方式访问成员,查询效率高
- 增删操作会给系统带来性能消耗[保证数据下标越界的问题,需要动态扩容]
长度为5的数组,添加1个节点,需要在原有数组的基础上创建一个长度为6的数组,把原来的内容复制过去,再添加新的内容;
删除时,创建一个长度为4的数组,把原来的数据再copy过去;
数组是有固定长度,所以要保证数据下表越界的问题,所以增删效率不高。
2. 链表
单向链表和双向链表
双向链表
- 灵活的空间要求,存储空间不要求连续
- 不支持下标访问,支持顺序遍历检索
- 针对增删效率比较高,只和操作的节点的前后节点有关系,无需移动元素
查询效率低,添加、删除节点效率高
查询:因为没有连续地址,按最短顺序,next —> prev 这样查找
删除:将节点next指向第三个的prev,并将第三个的prev指向第一个的next,中间的节点就会GC掉
添加:将上一个节点的next指向新节点的prev,将新节点的next指向下一个节点的prev
Java实现:LinkedList
private static class Node<E> { E item; //节点的元素
Node<E> next; //下一个节点
Node<E> prev; //上一个节点
Node(Node<E> prev, E element, Node<E> next) {
this.item = element;
this.next = next;
this.prev = prev;
}
}
3. 树
二叉树具有如下的特点:
- 某节点的左子树节点值仅包含小于该结点的值
- 某节点的右子树节点值仅包含大于该节点的值
- 左右子树每个也必须是二叉查找树
- 顺寻排列(从左到右)
平衡二叉树
特点:分布均匀,这样的树查找相对效率较高
不平衡二叉树
特点:分布不均匀,查询效率不高,相当于一个单向链表
面对这个问题,我们可以去除顶端优势(通过去除植物顶端优势,侧芽会迅速生长,慢慢变得强壮和平衡),红黑树其实就是去除二叉查找树顶端优势的解决方案,从而达到树的平衡,红黑树属于不完全二叉树。
3.1 红黑树
红黑树生成网站 https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
红黑树,Red-Black Tree[RBT]是一个自平衡【不是绝对】的二叉查找树,树上的节点满足如下的规则:
- 每个节点要么是红色,要么是黑色
- 根节点必须是黑色
- 每个叶子节点【NULL】是黑色
- 每个红色节点的两个子节点必须是黑色
- 任意节点到每个叶子节点的路径包含相同数量的黑色节点
黑平衡二叉树
- recolor 重新标志节点颜色
- rotation 旋转 树达到平衡的关键
红黑树能自平衡,他靠的是什么?三种操作:左旋、右旋和变色
左旋:以某个节点作为支点(旋转节点),其右子节点变为旋转节点的父节点,
右子节点的左子节点变为旋转节点的右子节点,左子节点保持不变。
右旋:以某个节点作为支点(旋转节点),其左子节点变为旋转节点的父节点,
左子节点的右子节点变为旋转节点的左子节点,右子节点保持不变。
变色:节点的颜色由红变黑或由黑变红
红黑树插入的场景
p=parent s=uncle pp=grand parent
二、集合
Coolection接口
类似于数组,存储相同类型
Map接口
键值对
Iterator 迭代
工具类:
Collections
Arrays
比较器
Comparable
Comparator
2.1 List集合
1. ArrayList
ArrayList本质上就是动态数组,支持动态扩容
/** * Default initial capacity.
* 默认的数组长度
*/
private static final int DEFAULT_CAPACITY = 10;
/**
* Shared empty array instance used for empty instances.
* 默认空数组
*/
private static final Object[] EMPTY_ELEMENTDATA = {};
/**
* Shared empty array instance used for default sized empty instances. We
* distinguish this from EMPTY_ELEMENTDATA to know how much to inflate when
* first element is added.
*/
private static final Object[] DEFAULTCAPACITY_EMPTY_ELEMENTDATA = {};
/**
* The array buffer into which the elements of the ArrayList are stored.
* The capacity of the ArrayList is the length of this array buffer. Any
* empty ArrayList with elementData == DEFAULTCAPACITY_EMPTY_ELEMENTDATA
* will be expanded to DEFAULT_CAPACITY when the first element is added.
* 集合中存储数据的数组对象
*/
transient Object[] elementData; // non-private to simplify nested class access
/**
* The size of the ArrayList (the number of elements it contains).
* 集合中元素的个数
* @serial
*/
private int size;
new ArrayList(?)初始操作
- 无参操作:
/** * Constructs an empty list with an initial capacity of ten.
*/
public ArrayList() {
this.elementData = DEFAULTCAPACITY_EMPTY_ELEMENTDATA;
// this.elementData = {}
}
- 有参操作:
/** * Constructs an empty list with the specified initial capacity.
*
* @param initialCapacity the initial capacity of the list
* @throws IllegalArgumentException if the specified initial capacity
* is negative
*/
public ArrayList(int initialCapacity) {
if (initialCapacity > 0) {
// 初始长度 > 0 就创建一个指定大小的数组
this.elementData = new Object[initialCapacity];
} else if (initialCapacity == 0) {
// 否则就将this.elementData = {}空数组
this.elementData = EMPTY_ELEMENTDATA;
} else {
throw new IllegalArgumentException("Illegal Capacity: "+
initialCapacity);
}
}
add()
add()
/** * Appends the specified element to the end of this list.
*
* @param e element to be appended to this list
* @return <tt>true</tt> (as specified by {@link Collection#add})
*/
public boolean add(E e) {
// 确定容量 动态扩容
ensureCapacityInternal(size + 1); // Increments modCount!!
// 将要添加的元素 添加到数组中 elementData[size] = e size = size + 1
elementData[size++] = e;
return true;
}
ensureCapacityInternal(int)
/** * elemmentData {}
* minCapacity 1
*/
private void ensureCapacityInternal(int minCapacity) {
ensureExplicitCapacity(calculateCapacity(elementData, minCapacity));
}
calculateCapacity(elementData, minCapacity)
private static int calculateCapacity(Object[] elementData, int minCapacity) { if (elementData == DEFAULTCAPACITY_EMPTY_ELEMENTDATA) { // elementData = {}
// DEFAULT_CAPACITY=10, minCapacity=1 return 10
return Math.max(DEFAULT_CAPACITY, minCapacity);
}
return minCapacity;
}
ensureExplicitCapacity(min)
private void ensureExplicitCapacity(int minCapacity) { modCount++; // 增长操作次数
// overflow-conscious code
if (minCapacity - elementData.length > 0)
grow(minCapacity);
}
grow(min)
private void grow(int minCapacity) { // overflow-conscious code
int oldCapacity = elementData.length;
int newCapacity = oldCapacity + (oldCapacity >> 1);
if (newCapacity - minCapacity < 0)
newCapacity = minCapacity;
if (newCapacity - MAX_ARRAY_SIZE > 0)
newCapacity = hugeCapacity(minCapacity);
// minCapacity is usually close to size, so this is a win:
// 第一次向空添加时会copy一个新长度为10的数组给elementData
elementData = Arrays.copyOf(elementData, newCapacity);
}
get()
get(index)
public E get(int index) { rangeCheck(index); // 检查索引
return elementData(index); // 返回数组中的对象
}
rangeCheck(index)
private void rangeCheck(int index) { if (index >= size)
throw new IndexOutOfBoundsException(outOfBoundsMsg(index));
}
elementData(index)
E elementData(int index) { return (E) elementData[index];
}
set()
set(index, value)
public E set(int index, E element) { rangeCheck(index); // 检查索引
E oldValue = elementData(index); // 获取原来的值
elementData[index] = element; // 将索引赋值为新值
return oldValue; // 返回旧值
}
remove()
remove(index)
public E remove(int index) { rangeCheck(index); // 检查索引
modCount++; // 操作+1
E oldValue = elementData(index); // 获取旧值
// 获取要移动的元素的个数
// {1,2,3,4,5,6,7,8,9} index=3时
// 9 - 3 - 1 = 5 要移动五个元素{5, 6, 7, 8, 9}
int numMoved = size - index - 1;
if (numMoved > 0)
// 参数说明:原数组,3+1{5},原数组,3,5个
// 在原数组索引为4的地方添加5个元素到原数组索引为3(从4开始)开始的地方
System.arraycopy(elementData, index+1, elementData, index,
numMoved);
// --size 并且将那个elementData[--size]指向null,等待GC处理原节点
elementData[--size] = null; // clear to let GC do its work
return oldValue;
}
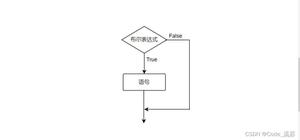
FailFast机制
集合为了保证在多线程的情况下,是线程安全的,给出一个快速失败的机制。
也不止多线程,在用Iterator遍历时,防止读的时候,进行add,remove的操作。
Java集合为了应对并发访问在集合迭代过程中,内部结构发生变化的一种防护措施,这种错误检查的机制为这种有可能发生错误,通过抛出java.util.ConcurrentModificationException
保证集合在遍历过程中在并发操作中的原子性
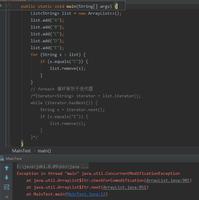
public E next() {checkForComodification();
int i = cursor;
if (i >= size)
throw new NoSuchElementException();
Object[] elementData = ArrayList.this.elementData;
if (i >= elementData.length)
throw new ConcurrentModificationException();
cursor = i + 1;
return (E) elementData[lastRet = i];
}
public void remove() {
if (lastRet < 0)
throw new IllegalStateException();
checkForComodification();
try {
ArrayList.this.remove(lastRet);
cursor = lastRet;
lastRet = -1;
expectedModCount = modCount;
} catch (IndexOutOfBoundsException ex) {
throw new ConcurrentModificationException();
}
}
checkForComodification()final void checkForComodification() {if (modCount != expectedModCount)
throw new ConcurrentModificationException();
}
2. LinkedList
LinkedList是通过双向链表去实现的,他的数据结构具有双向链表的优缺点,既然是双向链表,那么它的顺序访问效率会非常高,而随机访问的效率会比较低,它包含一个非常重要的私有的内部静态类。
private static class Node<E> {E item; // 节点的元素
Node<E> next; // 下一个节点
Node<E> prev; // 上一个节点
Node(Node<E> prev, E element, Node<E> next) {
this.item = element;
this.next = next;
this.prev = prev;
}
}
push(),add()
// push操作相当于在头节点插入 private void linkFirst(E e) {
final Node<E> f = first;
final Node<E> newNode = new Node<>(null, e, f);
first = newNode;
if (f == null)
last = newNode;
else
f.prev = newNode;
size++;
modCount++;
}
// add操作相当于向尾节点插入
void linkLast(E e) {
final Node<E> l = last;
final Node<E> newNode = new Node<>(l, e, null);
last = newNode;
if (l == null)
first = newNode;
else
l.next = newNode;
size++;
modCount++;
}
get()
本质上还是遍历链表中的数据
get(index)
public E get(int index) { checkElementIndex(index); // 检查索引
return node(index).item;
}
node(index)
Node<E> node(int index) { // assert isElementIndex(index);
if (index < (size >> 1)) { // 如果index < 一半,从前往后遍历
Node<E> x = first;
for (int i = 0; i < index; i++)
x = x.next;
return x;
} else { // 如果index > 一半,从后往前遍历
Node<E> x = last;
for (int i = size - 1; i > index; i--)
x = x.prev;
return x;
}
}
set()
public E set(int index, E element) { checkElementIndex(index); // 检查索引
Node<E> x = node(index); // 上面的node方法
E oldVal = x.item; // 获取原来的值
x.item = element; // 设置新的值
return oldVal; // 返回修改前的值
}
3. Vector(已过时)
和ArrayList很类似,都是以动态数组的形式来存储数据
线程安全的,都是同步方法synchronized,影响性能
public synchronized E set(int index, E element) { if (index >= elementCount)
throw new ArrayIndexOutOfBoundsException(index);
E oldValue = elementData(index);
elementData[index] = element;
return oldValue;
}
public synchronized boolean add(E e) {
modCount++;
ensureCapacityHelper(elementCount + 1);
elementData[elementCount++] = e;
return true;
}
Vector子类Stack
demo,判断字符串\'(\',\')\',\'{\',\'}\',\'[\',\']\'是否有效
public static boolean isValid(String s) { Stack<Character> stack = new Stack<>();
char[] sarr = s.toCharArray();
for (int i = 0; i < sarr.length; i++) {
if (sarr[i] == \'(\' || sarr[i] == \'{\' || sarr[i] == \'[\')
stack.push(sarr[i]);
if (stack.isEmpty())
return false;
if (sarr[i] == \')\' && \'(\' != stack.pop())
return false;
if (sarr[i] == \'}\' && \'{\' != stack.pop())
return false;
if (sarr[i] == \']\' && \'[\' != stack.pop())
return false;
}
return stack.isEmpty();
}
怎么让集合线程安全
Collections
CopyOnWriteArrayList
ArrayList想实现线程安全,除了可以Lock,synchronized之外,还可以用集合工具类的方法;
可以增加代码的灵活度,在我们需要同步时通过如下代码:
List syncList = Collections.synchronizedList(list);本质上:
public E get(int index) {synchronized (mutex) {return list.get(index);}
}
public E set(int index, E element) {
synchronized (mutex) {return list.set(index, element);}
}
public void add(int index, E element) {
synchronized (mutex) {list.add(index, element);}
}
public E remove(int index) {
synchronized (mutex) {return list.remove(index);}
}
在原来的基础上,做了一个同步代码块的包装
2.2 Set集合
1. HashSet简单介绍
概述
HashSet实现Set接口,由哈希表支持,他不保证set的迭代顺序,特别是不保证该顺序永久不变,允许使用null作为元素。
public HashSet() { map = new HashMap<>();
}
add()
add()
public boolean add(E e) { return map.put(e, PRESENT)==null;
}
本质上是将数据保存在HashMap中,key就是我们添加的内容,value就是我们定义的一个Object对象
特点
底层数据结构是哈希表,HashSet的本质是没有重复元素的集合,它是通过HashMap实现的,HashSet中含有一个HashMap类型的成员变量
map。
2. TreeSet
概述
基于TreeMap的NavigableSet实现,使用元素的自然顺序对元素进行排序,或者根据创建set时提供的Comparator进行排序,具体取决于使用的构造方法。
public TreeSet() { this(new TreeMap<E,Object>());
}
TreeSet(NavigableMap<E,Object> m) {
this.m = m;
}
add()
add()
public boolean add(E e) { return m.put(e, PRESENT)==null;
}
本质上是将数据保存在TreeMap中,key是我们添加的内容,value是一个固定Object对象。
PRESENT
// Dummy value to associate with an Object in the backing Mapprivate static final Object PRESENT = new Object();
2.3 Map集合
1. Map集合的特点
- 能够存储唯一的Key的数据(唯一,不可重复)Set
- 能够存储可以重复的数据(可重复) List
- 值的顺序取决于键的顺序
- 键和值都是可以存储null元素的
2. TreeMap
本质上就是红黑树的实现。
- 每个节点要么是红色,要么是黑色
- 根节点必须是黑色
- 每个叶子节点【NULL】是黑色
- 每个红色节点的两个子节点必须是黑色
- 任意节点到每个叶子节点的路径包含相同数量的黑节点
static final class Entry<K,V> implements Map.Entry<K,V> { K key; // 键
V value; // 值
Entry<K,V> left; // 左子节点
Entry<K,V> right; // 右子节点
Entry<K,V> parent; // 父节点
boolean color = BLACK; // 节点默认是黑色
......
}
put()
put()
public V put(K key, V value) { // 将root赋值给局部变量 null
Entry<K,V> t = root;
if (t == null) { // 初始操作
// 检查key是否为空
compare(key, key); // type (and possibly null) check
// 将要添加的key, value封装为一个entry对象,并赋值给root对象
root = new Entry<>(key, value, null);
size = 1;
modCount++;
// 第一次返回 空
return null;
}
int cmp; // 统计
Entry<K,V> parent; // 父节点
// split comparator and comparable paths
Comparator<? super K> cpr = comparator; // 比较器
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)
t = t.left;
else if (cmp > 0)
t = t.right;
else
return t.setValue(value);
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable<? super K> k = (Comparable<? super K>) key;
do {
// 第二次put,将root赋值给了parent
parent = t;
// 第二次,和root节点的值比较大小
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left; // 将父节点的左子节点给t
else if (cmp > 0)
t = t.right; // 将父节点的右子节点给t
else
// 直接修改值
return t.setValue(value);
} while (t != null);
}
// 将我们要插入的key value封装成一个Entry对象
Entry<K,V> e = new Entry<>(key, value, parent);
if (cmp < 0)
parent.left = e; // 插入的节点在parent节点的左侧
else
parent.right = e; // 插入的节点在parent节点右侧
// 实现红黑树的平衡
fixAfterInsertion(e);
size++;
modCount++;
return null;
}
// 根据源码分析能发现,第一次 put 时,只将root置为 (key, value, null)
// 第二次会创建一个parent = root,如果newKey < key,将t置为t.left,反之t置为t.right,直到t == null时,跳出循环,当前t为parent的或左或右的子节点
// 判断是左还是右,将或左或右子节点 = new Entry(newKey, newValue, parent);
fixAfterInsertion(e)
private void fixAfterInsertion(Entry<K,V> x) { // 设置添加节点的颜色为红色
x.color = RED;
// 循环条件:添加的节点不为空,不是root节点,父节点的颜色为红色
while (x != null && x != root && x.parent.color == RED) {
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) { // 父节点 是否是 祖父节点的左子节点
Entry<K,V> y = rightOf(parentOf(parentOf(x))); // 祖父节点的右子节点,是判断条件中的parentof(x)的兄弟节点,当前节点的叔叔节点
if (colorOf(y) == RED) { // 叔叔节点是红色,直接变色
setColor(parentOf(x), BLACK); // 设置父节点为黑色
setColor(y, BLACK); // 设置叔叔节点的颜色为黑色
setColor(parentOf(parentOf(x)), RED); // 设置祖父节点的颜色为红色
x = parentOf(parentOf(x)); // 将祖父节点设置为要插入的节点
} else { // 叔叔节点是黑色
if (x == rightOf(parentOf(x))) { // 当前节点是父节点的右节点
x = parentOf(x); // 将父节点设置为要插入的节点
rotateLeft(x); // 将父节点左旋
}
setColor(parentOf(x), BLACK); // 祖父节点设置为黑色
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
} else {
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
root.color = BLACK;
}
3. HashMap
HashMap简单介绍
HashMap底层结构:
- Jdk1.7及以前是采用数组 + 链表
- Jdk1.8之后 采用数组 + 链表 或者 数组 + 红黑树方式进行元素的存储,存储在HashMap集合中的元素都将是一个Map.Entry的内部接口的实现
实现原理:
- 数组中存放的是hash值相同的key,重复hash值的key可能有多个
- key之间是以双向链表实现的,但是双向链表的查询效率比较低,为了提高查询效率,在链表的长度等于8的时候,会把链表转换为红黑树,目的就是为了提升查询效率。
HashMap的成员变量
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // 默认的HashMap中数组的长度 16static final int MAXIMUM_CAPACITY = 1 << 30; // HashMap最大容量
static final float DEFAULT_LOAD_FACTOR = 0.75f; // 默认扩容平衡因子 当前数组长度为16,如果数组内占用达到3/4时,也就是12个的时候,会进行扩容
static final int TREEIFY_THRESHOLD = 8; // 链表转红黑树的临界值,当链表长度为8时,会转成红黑树
static final int UNTREEIFY_THRESHOLD = 6; // 红黑树转列表的临界值,当红黑树的内容少于等于6的时候,会转成列表
static final int MIN_TREEIFY_CAPACITY = 64; // 链表转红黑树的数组长度的临界值,当数组的长度 !> 64个的时候,即使达到TREEIFY_THRESHOLD也不会转换
transient Node<K,V>[] table; // hashMap中的数组结构
transient int size; // HashMap中的元素个数
transient int modCount; // 对HashMap擦欧总的次数
int threshold; // 扩容的临界值
final float loadFactor; // 实际的扩容值
put()
put()
public V put(K key, V value) { return putVal(hash(key), key, value, false, true);
}
hash(key):获取key对的hash值
static final int hash(Object key) { int h;
/**
* key.hashCode() 32长度的二进制的值
* h向右移动16位
* 两个值异或处理
*/
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
为什么要右移16位?
- 后面代码会讲到:代码中遇到&运算,如果不右移16位,会造成很容易得到0,会造成散列分布不均匀
putVal(int, K, V, false, true)
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0) // 初始判断
/**
* resize() 初始数组,扩容
* n:记录数组长度
* 第一次,获取一个容量为16的数组,见下方resize()源码
*/
n = (tab = resize()).length; // 第一次 n=16
// 初始:确定插入的key在数组中的下标 0~15
// (tab[1111 & hash] == null) 突然发现 \'&\'运算很神奇!
if ((p = tab[i = (n - 1) & hash]) == null)
// 通过hash值找到的数组下标里面没有内容,直接赋值
tab[i] = newNode(hash, key, value, null);
else { // 通过hash值找到的数组下标里面有内容
Node<K,V> e; K k;
// 与数组中这个节点的hash值作比较
// 并且与链表第一个node的key作比较,如果相同,那么直接p赋值给e
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
// 如果是个RedBlackTree
else if (p instanceof TreeNode)
// 类似TreeMap
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
// 其他则是普通链表
else {
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) { // 链表的尾部
p.next = newNode(hash, key, value, null); // 将新节点添加到了链表的尾部
// 判断是否满足binCount >= 7,转红黑树
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash); // 具体转链表转红黑树,参见下面treeifyBin(tab, hash)源码
break;
}
// 不在链表尾部,并且hash值相等,Key相同,跳出循环,将用e作为被修改内容的节点
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e; // 给p刷新为p的next节点
}
}
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
resize()
// 获取下一个节点时,由于next = e.next,多线程时容易造成死循环// 由此也可得出,HashMap是线程不安全的
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
// 第一次 oldCap = 0
// 第二次 oldCap = 16
int oldCap = (oldTab == null) ? 0 : oldTab.length;
// 原来的扩容因子 第一次为0
// 第二次扩容为 16*0,75 = 12
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) { // 从第二次开始执行
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
// newCap = 32 < 2^30 && 16 >= 16
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
// 新的容量是原来的两倍 newThr = 24
newThr = oldThr << 1; // double threshold
}
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
else { // zero initial threshold signifies using defaults
// 初始时执行:
// 新的数组容量16
newCap = DEFAULT_INITIAL_CAPACITY;
// 新的扩容因子 0.75 * 16 = 12
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr; // 第一次更新了扩容的临界值 12
@SuppressWarnings({"rawtypes","unchecked"})
// 第一次创建了一个容量为16的Node数组
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab; // 更新HashMap中的数组结构
if (oldTab != null) { // 初始不执行,第二次执行
for (int j = 0; j < oldCap; ++j) { // 该循环为了平衡数组中节点上的数据
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null) // 表示数组当前位置只有一个节点,将数组原来位置上的节点移到新的位置上
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode) // 如果当前节点是个红黑树
((TreeNode<K,V>)e).split(this, newTab, j, oldCap); // 移动红黑树节点,把整个节点进行处理替换
else { // preserve order 整个列表的移动,把链表分开移动到不同的节点上
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
treeifyBin(tab, hash)
final void treeifyBin(Node<K,V>[] tab, int hash) { int n, index; Node<K,V> e;
// 前提:链表长度>=8
// 如果tab为空,或者这个tab数组的长度 < 64
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
resize(); // 扩容
else if ((e = tab[index = (n - 1) & hash]) != null) {
// 链表转红黑树的逻辑
TreeNode<K,V> hd = null, tl = null;
do {
TreeNode<K,V> p = replacementTreeNode(e, null);
if (tl == null)
hd = p;
else {
p.prev = tl;
tl.next = p;
}
tl = p;
} while ((e = e.next) != null);
if ((tab[index] = hd) != null)
hd.treeify(tab);
}
}
HashMap.put()总结
以上是 红黑树与数据结构在Java集合中的应用 的全部内容, 来源链接: utcz.com/z/391244.html