算法练习2---斐波那契数列java版

  • Z时代
  • 2024-01-10
  • 分类：综合

java

古典问题：有一对兔子，从出生后第3个月起每个月都生一对兔子，小兔子长到第四个月后每个月又生一对兔子， 假如兔子都不死，问每个月的兔子总数为多少？

数列：1   1   2   3   5   8   13......

可以总结出公示为F(n)=F(n-1)+F(n-2)

java程序代码实现如下：

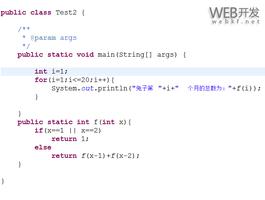
public class ArithTest {
    public static void main(String[] args) {
        ArithTest at = new ArithTest();
        // 算法一：显示前20个月每月兔子数量
        for(int n=1;n<=20;n++){
            System.out.println("第"+n+"个月兔子数量为"+at.f(n));
        }
    /* 算法一：斐波那契数列
     * 古典问题：有一对兔子，从出生后第3个月起每个月都生一对兔子，小兔子长到第四个月后每个月又生一对兔子， 假如兔子都不死，问每个月的兔子总数为多少？
     * 规律：1 1 2 3 5 8 13 ...
     * f(n)=f(n-1)+f(n-2)
     */
    public int f(int n){
        if(n==1|n==2){
            return 1;
        }else{
            return f(n-1)+f(n-2);
        }
    }
}

执行结果为：

第1个月兔子数量为1
第2个月兔子数量为1
第3个月兔子数量为2
第4个月兔子数量为3
第5个月兔子数量为5
第6个月兔子数量为8
第7个月兔子数量为13
第8个月兔子数量为21
第9个月兔子数量为34
第10个月兔子数量为55
第11个月兔子数量为89
第12个月兔子数量为144
第13个月兔子数量为233
第14个月兔子数量为377
第15个月兔子数量为610
第16个月兔子数量为987
第17个月兔子数量为1597
第18个月兔子数量为2584
第19个月兔子数量为4181
第20个月兔子数量为6765

以上是 算法练习2---斐波那契数列java版 的全部内容， 来源链接： utcz.com/z/390033.html

回到顶部