什么是编译器设计中的搜索树和哈希表?
搜索树
一种更有效的符号表组织技术是向每条记录添加两个链接字段 LEFT 和 RIGHT。我们使用这些字段将记录链接到二叉搜索树中。
这棵树的特性是,所有名称 NAME (j) 从 NAME (i) 可通过链接 LEFT (i) 访问,然后按照任何链接序列将按字母顺序排列在 NAME (i) 之前(象征性地,NAME (j) <姓名 (i))
类似地,所有以 RIGHT (i) 开头可访问的名称 NAME (k) 将具有 NAME (i) < NAME (k) 的属性。因此,如果我们正在搜索 NAME 并找到了 NAME (i) 的记录,我们只需要在 NAME < NAME (i) 时遵循 LEFT (i) 并且如果 NAME (i) < NAME (i) 只需要遵循 RIGHT (i)当然,如果 NAME =NAME(i)我们找到了我们正在寻找的东西。
二叉搜索树算法
最初,Ptr 将指向树的根。
虽然 Ptr ≠ NULL 做
如果 NAME = NAME (Ptr)
然后返回真
else if NAME<NAME (Ptr) then
Ptr-LEFT(Ptr)
否则 Ptr-= RIGHT (Ptr)
循环结束
复杂
如果以随机顺序遇到名称,则树中路径的平均长度将与 log n 成正比,其中 n 是名称的数量。因此每次搜索都从根开始走一条路径,输入n个名字并进行m个查询所需的预期时间与(n + m)log n成正比,如果n大于50左右,则二分搜索有明显的优势树在链表上,也可能在链接的自组织表上。
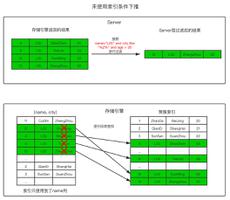
哈希表
散列是用于搜索符号表记录的重要过程。这种方法优于列表组织。
在散列方案中,维护了两个表
哈希表
符号表
哈希表由从 0 到 K-1 的 K 个条目组成。这些条目是指向符号表的指针,指向符号表的名称。它可以决定 "Name" 是否在符号表中,我们使用哈希函数 'h' 包括 h (Name) 将产生 0 到 K - 1 之间的整数。我们可以通过 position = 搜索任何名称h(Name)。
使用这个位置,我们可以访问符号表中名称的确切位置。
散列函数应该导致名称在符号表中的分布。散列函数应该是最小的碰撞次数。冲突是散列函数导致存储名称的位置相同的情况。有多种冲突解决技术是开放寻址、链接和重新散列。
复杂
对于我们选择的任何常数 k,该方案提供了在与 n(n + m)/k 成比例的时间内对 n 个名称执行 m 访问的能力。因为 k 可以做得像我们喜欢的一样大。这种方法通常优于线性列表或搜索树,并且在大多数情况下是符号表的可选技术,尤其是在存储成本不是很高的情况下。
以上是 什么是编译器设计中的搜索树和哈希表? 的全部内容, 来源链接: utcz.com/z/363459.html