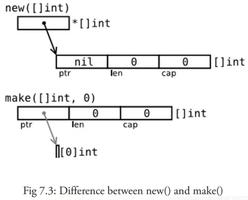
运算符优先文法的 LEADING 和 TRAILING 操作是什么?
领导
如果产生式的形式是 A → aα 或 A → Ba α,其中 B 是非终结符,并且 α 可以是任何字符串,那么 RHS 上的第一个终结符是
Leading(A) = {一}
如果生产的形式是 A → Bα,如果 a 在 LEADING (B) 中,那么 a 也将在 LEADING (A) 中。
尾随
如果产生式的形式为 A→ αa 或 A → αaB,其中 B 是非终结符,并且 α 可以是任何字符串,那么,
尾随 (A) = {a}
如果生产形式为 A → αB。如果 a 在 TRAILING (B) 中,则 a 将在 TRAILING (A) 中。
计算 LEADING 的算法
输入- 上下文无关语法 G
输出− LEADING (A) = {a} iff 布尔数组 L [A, a] = true
Method - Procedure Install (A, a) 将使 L (A, a) 为真,如果之前不是真的。
开始
对于每个非终端 A 和终端 a
L [A, a] = false ;
对于形式 A ⟶ aα 或 A → B a α 的每个产生式
安装 (A, a) ;
虽然堆栈不为空
弹出顶对 (B, a) 形成 Stack ;
对于形式 A → B 的每个产生式 α
安装 (A, a);
结尾
程序 安装 (A, a)
开始
如果不是 L [A, a] 那么
L [A, a] = 真
将 (A, a) 压入堆栈。
结尾
计算TRAILING的算法
输入- 上下文无关语法 G
输出− TRAILING (A) = {a} iff 布尔数组 T [A, a] = true
方法
开始
对于每个非终端 A 和终端 a
T [A, a] = false ;
对于形式 A ⟶ αa 或 A → α a B 的每个产生式
安装 (A, a) ;
虽然堆栈不为空
弹出顶对 (B, a) 形成 Stack ;
对于形式 A → αB 的每个产生式
安装 (A, a);
结尾
程序 安装 (A, a)
开始
如果不是 T [A, a] 那么
T [A, a] = 真
将 (A, a) 压入堆栈。
结尾
计算运算符优先关系的算法
输入- 运算符语法
输出- 终端和符号之间的优先关系。
方法
开始
对于每个产生式 A → B 1 , B 2 , … … … 。乙ñ
对于 i = 1 到 n – 1
如果 B i和 B i+1都是终端,那么
设置 B i = B i+1
如果 i ≤ n − 2 且 B i和 B i+2都是终结符,而 B i+1是非终结符,则
设置 B i = B i+1
如果 B i是终结符 & B i+1是非终结符,那么对于 LEADING (B i+1 ) 中的所有 a
设置 B i <。一种
如果 B i是非终结符 & B i+1是终结符,那么对于 TRAILING (B i ) 中的所有 a
设置一个 . > B i+1
结尾
以上是 运算符优先文法的 LEADING 和 TRAILING 操作是什么? 的全部内容, 来源链接: utcz.com/z/362124.html