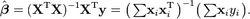scikit-learn线性回归,多元回归,多项式回归的实现
匹萨的直径与价格的数据
%matplotlib inline
import matplotlib.pyplot as plt
def runplt():
plt.figure()
plt.title(u'diameter-cost curver')
plt.xlabel(u'diameter')
plt.ylabel(u'cost')
plt.axis([0, 25, 0, 25])
plt.grid(True)
return plt
plt = runplt()
X = [[6], [8], [10], [14], [18]]
y = [[7], [9], [13], [17.5], [18]]
plt.plot(X, y, 'k.')
plt.show()
训练模型
from sklearn.linear_model import LinearRegression
import numpy as np
# 创建并拟合模型
model = LinearRegression()
model.fit(X, y)
print('预测一张12英寸匹萨价格:$%.2f' % model.predict(np.array([12]).reshape(-1, 1))[0])
预测一张12英寸匹萨价格:$13.68
一元线性回归假设解释变量和响应变量之间存在线性关系;这个线性模型所构成的空间是一个超平面(hyperplane)。
超平面是n维欧氏空间中余维度等于一的线性子空间,如平面中的直线、空间中的平面等,总比包含它的空间少一维。
在一元线性回归中,一个维度是响应变量,另一个维度是解释变量,总共两维。因此,其超平面只有一维,就是一条线。
上述代码中sklearn.linear_model.LinearRegression类是一个估计器(estimator)。估计器依据观测值来预测结果。在scikit-learn里面,所有的估计器都带有:
- fit()
- predict()
fit()用来分析模型参数,predict()是通过fit()算出的模型参数构成的模型,对解释变量进行预测获得的值。
因为所有的估计器都有这两种方法,所有scikit-learn很容易实验不同的模型。
一元线性回归模型:
一元线性回归拟合模型的参数估计常用方法是:
- 普通最小二乘法(ordinary least squares )
- 线性最小二乘法(linear least squares)
首先,我们定义出拟合成本函数,然后对参数进行数理统计。
plt = runplt()
plt.plot(X, y, 'k.')
X2 = [[0], [10], [14], [25]]
model = LinearRegression()
model.fit(X, y)
y2 = model.predict(X2)
plt.plot(X, y, 'k.')
plt.plot(X2, y2, 'g-')
plt.show()
plt = runplt()
plt.plot(X, y, 'k.')
y3 = [14.25, 14.25, 14.25, 14.25]
y4 = y2 * 0.5 + 5
model.fit(X[1:-1], y[1:-1])
y5 = model.predict(X2)
plt.plot(X, y, 'k.')
plt.plot(X2, y2, 'g-.')
plt.plot(X2, y3, 'r-.')
plt.plot(X2, y4, 'y-.')
plt.plot(X2, y5, 'o-')
plt.show()
成本函数(cost function)也叫损失函数(loss function),用来定义模型与观测值的误差。模型预测的价格与训练集数据的差异称为残差(residuals)或训练误差(training errors)。后面我们会用模型计算测试集,那时模型预测的价格与测试集数据的差异称为预测误差(prediction errors)或训练误差(test errors)。
模型的残差是训练样本点与线性回归模型的纵向距离,如下图所示:
plt = runplt()
plt.plot(X, y, 'k.')
X2 = [[0], [10], [14], [25]]
model = LinearRegression()
model.fit(X, y)
y2 = model.predict(X2)
plt.plot(X, y, 'k.')
plt.plot(X2, y2, 'g-')
# 残差预测值
yr = model.predict(X)
for idx, x in enumerate(X):
plt.plot([x, x], [y[idx], yr[idx]], 'r-')
plt.show()
我们可以通过残差之和最小化实现最佳拟合,也就是说模型预测的值与训练集的数据最接近就是最佳拟合。对模型的拟合度进行评估的函数称为残差平方和(residual sum of squares)成本函数。就是让所有训练数据与模型的残差的平方之和最小化,如下所示:
其中,
import numpy as np
print('残差平方和: %.2f' % np.mean((model.predict(X) - y) ** 2))
残差平方和: 1.75
解一元线性回归的最小二乘法
通过成本函数最小化获得参数,我们先求相关系数 ββ 。按照频率论的观点,我们首先需要计算 xx 的方差和 xx 与 yy 的协方差。
方差是用来衡量样本分散程度的。如果样本全部相等,那么方差为0。方差越小,表示样本越集中,反正则样本越分散。方差计算公式如下:
Numpy里面有var方法可以直接计算方差,ddof参数是贝塞尔(无偏估计)校正系数(Bessel's correction),设置为1,可得样本方差无偏估计量。
print(np.var([6, 8, 10, 14, 18], ddof=1))
23.2
协方差表示两个变量的总体的变化趋势。如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。如果两个变量不相关,则协方差为0,变量线性无关不表示一定没有其他相关性。协方差公式如下:
其中,
import numpy as np
print(np.cov([6, 8, 10, 14, 18], [7, 9, 13, 17.5, 18])[0][1])
22.65
现在有了方差和协方差,就可以计算相关系统
算出
将前面的数据带入公式就可以求出
模型评估
前面我们用学习算法对训练集进行估计,得出了模型的参数。有些度量方法可以用来评估预测效果,我们用R方(r-squared)评估匹萨价格预测的效果。R方也叫确定系数(coefficient of determination),表示模型对现实数据拟合的程度。计算R方的方法有几种。一元线性回归中R方等于皮尔逊积矩相关系数(Pearson product moment correlation coefficient或Pearson's r)的平方。种方法计算的R方一定介于0~1之间的正数。其他计算方法,包括scikit-learn中的方法,不是用皮尔逊积矩相关系数的平方计算的,因此当模型拟合效果很差的时候R方会是负值。下面我们用scikit-learn方法来计算R方。
R方是0.6620说明测试集里面过半数的价格都可以通过模型解释。现在,让我们用scikit-learn来验证一下。LinearRegression的score方法可以计算R方:
# 测试集
X_test = [[8], [9], [11], [16], [12]]
y_test = [[11], [8.5], [15], [18], [11]]
model = LinearRegression()
model.fit(X, y)
model.score(X_test, y_test)
0.66200528638545164
多元回归
from sklearn.linear_model import LinearRegression
X = [[6, 2], [8, 1], [10, 0], [14, 2], [18, 0]]
y = [[7], [9], [13], [17.5], [18]]
model = LinearRegression()
model.fit(X, y)
X_test = [[8, 2], [9, 0], [11, 2], [16, 2], [12, 0]]
y_test = [[11], [8.5], [15], [18], [11]]
predictions = model.predict(X_test)
for i, prediction in enumerate(predictions):
print('Predicted: %s, Target: %s' % (prediction, y_test[i]))
print('R-squared: %.2f' % model.score(X_test, y_test))
Predicted: [ 10.06250019], Target: [11]
Predicted: [ 10.28125019], Target: [8.5]
Predicted: [ 13.09375019], Target: [15]
Predicted: [ 18.14583353], Target: [18]
Predicted: [ 13.31250019], Target: [11]
R-squared: 0.77
上例中,我们假设解释变量和响应变量的关系是线性的。真实情况未必如此。下面我们用多项式回归,一种特殊的多元线性回归方法,增加了指数项。现实世界中的曲线关系都是通过增加多项式实现的,其实现方式和多元线性回归类似。本例还用一个解释变量,匹萨直径。让我们用下面的数据对两种模型做个比较:
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
X_train = [[6], [8], [10], [14], [18]]
y_train = [[7], [9], [13], [17.5], [18]]
X_test = [[6], [8], [11], [16]]
y_test = [[8], [12], [15], [18]]
# 建立线性回归,并用训练的模型绘图
regressor = LinearRegression()
regressor.fit(X_train, y_train)
xx = np.linspace(0, 26, 100)
yy = regressor.predict(xx.reshape(xx.shape[0], 1))
plt = runplt()
plt.plot(X_train, y_train, 'k.')
plt.plot(xx, yy)
quadratic_featurizer = PolynomialFeatures(degree=2)
X_train_quadratic = quadratic_featurizer.fit_transform(X_train)
X_test_quadratic = quadratic_featurizer.transform(X_test)
regressor_quadratic = LinearRegression()
regressor_quadratic.fit(X_train_quadratic, y_train)
xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0], 1))
plt.plot(xx, regressor_quadratic.predict(xx_quadratic), 'r-')
plt.show()
print(X_train)
print(X_train_quadratic)
print(X_test)
print(X_test_quadratic)
print('1 r-squared', regressor.score(X_test, y_test))
print('2 r-squared', regressor_quadratic.score(X_test_quadratic, y_test))
[[6], [8], [10], [14], [18]]
[[ 1. 6. 36.]
[ 1. 8. 64.]
[ 1. 10. 100.]
[ 1. 14. 196.]
[ 1. 18. 324.]]
[[6], [8], [11], [16]]
[[ 1. 6. 36.]
[ 1. 8. 64.]
[ 1. 11. 121.]
[ 1. 16. 256.]]
('1 r-squared', 0.80972683246686095)
('2 r-squared', 0.86754436563450732)
plt = runplt()
plt.plot(X_train, y_train, 'k.')
quadratic_featurizer = PolynomialFeatures(degree=2)
X_train_quadratic = quadratic_featurizer.fit_transform(X_train)
X_test_quadratic = quadratic_featurizer.transform(X_test)
regressor_quadratic = LinearRegression()
regressor_quadratic.fit(X_train_quadratic, y_train)
xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0], 1))
plt.plot(xx, regressor_quadratic.predict(xx_quadratic), 'r-')
cubic_featurizer = PolynomialFeatures(degree=3)
X_train_cubic = cubic_featurizer.fit_transform(X_train)
X_test_cubic = cubic_featurizer.transform(X_test)
regressor_cubic = LinearRegression()
regressor_cubic.fit(X_train_cubic, y_train)
xx_cubic = cubic_featurizer.transform(xx.reshape(xx.shape[0], 1))
plt.plot(xx, regressor_cubic.predict(xx_cubic))
plt.show()
print(X_train_cubic)
print(X_test_cubic)
print('2 r-squared', regressor_quadratic.score(X_test_quadratic, y_test))
print('3 r-squared', regressor_cubic.score(X_test_cubic, y_test))
[[ 1.00000000e+00 6.00000000e+00 3.60000000e+01 2.16000000e+02]
[ 1.00000000e+00 8.00000000e+00 6.40000000e+01 5.12000000e+02]
[ 1.00000000e+00 1.00000000e+01 1.00000000e+02 1.00000000e+03]
[ 1.00000000e+00 1.40000000e+01 1.96000000e+02 2.74400000e+03]
[ 1.00000000e+00 1.80000000e+01 3.24000000e+02 5.83200000e+03]]
[[ 1.00000000e+00 6.00000000e+00 3.60000000e+01 2.16000000e+02]
[ 1.00000000e+00 8.00000000e+00 6.40000000e+01 5.12000000e+02]
[ 1.00000000e+00 1.10000000e+01 1.21000000e+02 1.33100000e+03]
[ 1.00000000e+00 1.60000000e+01 2.56000000e+02 4.09600000e+03]]
('2 r-squared', 0.86754436563450732)
('3 r-squared', 0.83569241560369567)
plt = runplt()
plt.plot(X_train, y_train, 'k.')
quadratic_featurizer = PolynomialFeatures(degree=2)
X_train_quadratic = quadratic_featurizer.fit_transform(X_train)
X_test_quadratic = quadratic_featurizer.transform(X_test)
regressor_quadratic = LinearRegression()
regressor_quadratic.fit(X_train_quadratic, y_train)
xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0], 1))
plt.plot(xx, regressor_quadratic.predict(xx_quadratic), 'r-')
seventh_featurizer = PolynomialFeatures(degree=7)
X_train_seventh = seventh_featurizer.fit_transform(X_train)
X_test_seventh = seventh_featurizer.transform(X_test)
regressor_seventh = LinearRegression()
regressor_seventh.fit(X_train_seventh, y_train)
xx_seventh = seventh_featurizer.transform(xx.reshape(xx.shape[0], 1))
plt.plot(xx, regressor_seventh.predict(xx_seventh))
plt.show()
print('2 r-squared', regressor_quadratic.score(X_test_quadratic, y_test))
print('7 r-squared', regressor_seventh.score(X_test_seventh, y_test))
('2 r-squared', 0.86754436563450732)
('7 r-squared', 0.49198460568655)
可以看出,七次拟合的R方值更低,虽然其图形基本经过了所有的点。可以认为这是拟合过度(over-fitting)的情况。这种模型并没有从输入和输出中推导出一般的规律,而是记忆训练集的结果,这样在测试集的测试效果就不好了。
正则化
LASSO方法会产生稀疏参数,大多数相关系数会变成0,模型只会保留一小部分特征。而岭回归还是会保留大多数尽可能小的相关系数。当两个变量相关时,LASSO方法会让其中一个变量的相关系数会变成0,而岭回归是将两个系数同时缩小。
import numpy as np
from sklearn.datasets import load_boston
from sklearn.linear_model import SGDRegressor
from sklearn.cross_validation import cross_val_score
from sklearn.preprocessing import StandardScaler
from sklearn.cross_validation import train_test_split
data = load_boston()
X_train, X_test, y_train, y_test = train_test_split(data.data, data.target)
X_scaler = StandardScaler()
y_scaler = StandardScaler()
X_train = X_scaler.fit_transform(X_train)
y_train = y_scaler.fit_transform(y_train.reshape(-1, 1))
X_test = X_scaler.transform(X_test)
y_test = y_scaler.transform(y_test.reshape(-1, 1))
regressor = SGDRegressor(loss='squared_loss',penalty="l1")
scores = cross_val_score(regressor, X_train, y_train.reshape(-1, 1), cv=5)
print('cv R', scores)
print('mean of cv R', np.mean(scores))
regressor.fit_transform(X_train, y_train)
print('Test set R', regressor.score(X_test, y_test))
('cv R', array([ 0.74761441, 0.62036841, 0.6851797 , 0.63347999, 0.79476346]))
('mean of cv R', 0.69628119572104885)
('Test set R', 0.75084948718041566)
以上是 scikit-learn线性回归,多元回归,多项式回归的实现 的全部内容, 来源链接: utcz.com/z/356782.html