Ruby实现的各种排序算法
时间复杂度:Θ(n^2)
Bubble sort
def bubble_sort(a)
(a.size-2).downto(0) do |i|
(0..i).each do |j|
a[j], a[j+1] = a[j+1], a[j] if a[j] > a[j+1]
end
end
return a
end
Selection sort
def selection_sort(a)
b = []
a.size.times do |i|
min = a.min
b << min
a.delete_at(a.index(min))
end
return b
end
Insertion sort
def insertion_sort(a)
a.each_with_index do |el,i|
j = i - 1
while j >= 0
break if a[j] <= el
a[j + 1] = a[j]
j -= 1
end
a[j + 1] = el
end
return a
end
Shell sort
def shell_sort(a)
gap = a.size
while(gap > 1)
gap = gap / 2
(gap..a.size-1).each do |i|
j = i
while(j > 0)
a[j], a[j-gap] = a[j-gap], a[j] if a[j] <= a[j-gap]
j = j - gap
end
end
end
return a
end
时间复杂度:Θ(n*logn)
Merge sort
def merge(l, r)
result = []
while l.size > 0 and r.size > 0 do
if l.first < r.first
result << l.shift
else
result << r.shift
end
end
if l.size > 0
result += l
end
if r.size > 0
result += r
end
return result
end
def merge_sort(a)
return a if a.size <= 1
middle = a.size / 2
left = merge_sort(a[0, middle])
right = merge_sort(a[middle, a.size - middle])
merge(left, right)
end
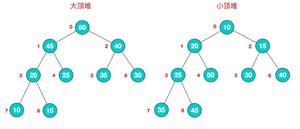
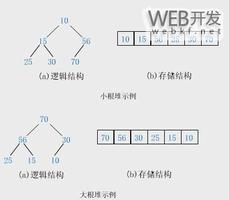
Heap sort
def heapify(a, idx, size)
left_idx = 2 * idx + 1
right_idx = 2 * idx + 2
bigger_idx = idx
bigger_idx = left_idx if left_idx < size && a[left_idx] > a[idx]
bigger_idx = right_idx if right_idx < size && a[right_idx] > a[bigger_idx]
if bigger_idx != idx
a[idx], a[bigger_idx] = a[bigger_idx], a[idx]
heapify(a, bigger_idx, size)
end
end
def build_heap(a)
last_parent_idx = a.length / 2 - 1
i = last_parent_idx
while i >= 0
heapify(a, i, a.size)
i = i - 1
end
end
def heap_sort(a)
return a if a.size <= 1
size = a.size
build_heap(a)
while size > 0
a[0], a[size-1] = a[size-1], a[0]
size = size - 1
heapify(a, 0, size)
end
return a
end
以上是 Ruby实现的各种排序算法 的全部内容, 来源链接: utcz.com/z/334314.html