拓扑排序

• Z时代
• 2024-01-10
• 分类：综合

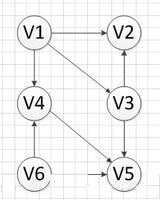
有向无环图的拓扑排序是顶点的线性排序。对于有向图的每条边 UV，顶点 u 将在排序中出现在顶点 v 之前。

我们知道源顶点会在目标顶点之后，所以我们需要使用堆栈来存储之前的元素。完成所有节点后，我们可以简单地从堆栈中显示它们。

输入和输出

Input:
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 1 0 0
0 1 0 0 0 0
1 1 0 0 0 0
1 0 1 0 0 0
Output:
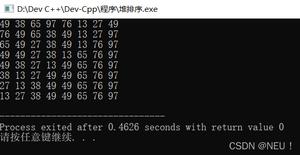
拓扑排序后的节点： 5 4 2 3 1 0

算法

topoSort(u, visited, stack)

输入 -起始顶点 u，一个数组，用于跟踪访问或未访问哪个节点。用于存储节点的堆栈。
输出 -在堆栈中按拓扑序列对顶点进行排序。

Begin
   mark u as visited
   for all vertices v which is adjacent with u, do
      if v is not visited, then
         topoSort(c, visited, stack)
   done
   push u into a stack
End

performTopologicalSorting(Graph)

输入 -给定的有向无环图。
输出 -节点序列。

Begin
   initially mark all nodes as unvisited
   for all nodes v of the graph, do
      if v is not visited, then
         topoSort(i, visited, stack)
   done
   pop and print all elements from the stack
End.

示例

#include<iostream>
#include<stack>
#define NODE 6
using namespace std;
int graph[NODE][NODE] = {
   {0, 0, 0, 0, 0, 0},
   {0, 0, 0, 0, 0, 0},
   {0, 0, 0, 1, 0, 0},
   {0, 1, 0, 0, 0, 0},
   {1, 1, 0, 0, 0, 0},
   {1, 0, 1, 0, 0, 0}
};
void topoSort(int u, bool visited[], stack<int>&stk) {
   visited[u] = true;                //设置为节点 v 被访问
   for(int v = 0; v<NODE; v++) {
      if(graph[u][v]) {             //对于与 u 相邻的所有顶点 v
         if(!visited[v])
            topoSort(v, visited, stk);
      }
   }
   stk.push(u);     //将起始顶点压入堆栈
}
void performTopologicalSort() {
   stack<int> stk;
   bool vis[NODE];
   for(int i = 0; i<NODE; i++)
      vis[i] = false;     //最初所有节点都未被访问
   for(int i = 0; i<NODE; i++)
      if(!vis[i])     //当节点未被访问时
         topoSort(i, vis, stk);
   while(!stk.empty()) {
      cout << stk.top() << " ";
      stk.pop();
   }
}
main() {
   cout << "拓扑排序后的节点： ";
   performTopologicalSort();
}

拓扑排序后的节点： 5 4 2 3 1 0

以上是 拓扑排序 的全部内容， 来源链接： utcz.com/z/331877.html