查找一个整数X,该整数除C中数组中仅一个元素外的所有元素的除数
概念
对于给定的整数数组,我们的任务是确定一个整数B,该整数B除给定数组中仅一个元素外的所有整数的因数。
应该注意的是,所有要素的GCD都不是1。
输入值
arr[] = {8, 16, 4, 24}输出结果
88 is the divisor of all except 4.
输入值
arr[] = {50, 15, 40, 41}输出结果
55 is the divisor of all except 41.
方法
我们创建一个前缀数组A,使位置或索引i包含从1到i的所有元素的GCD。以类似的方式,创建后缀数组C,使索引i包含从i到n-1(最后一个索引)的所有元素的GCD。已经看到,如果A [i-1]和C [i + 1]的GCD不是i元素的除数,那么它就是必需的答案。
示例
// C++ program to find the divisor of all//除了数组中的一个元素。
#include <bits/stdc++.h>
using namespace std;
//显示返回所有除数的函数
//除了数组中的一个元素。
int getDivisor1(int a1[], int n1){
//如果数组中只有一个元素
if (n1 == 1)
return (a1[0] + 1);
int A[n1], C[n1];
//现在创建GCD的前缀数组
A[0] = a1[0];
for (int i = 1; i < n1; i++)
A[i] = __gcd(a1[i], A[i - 1]);
//现在创建GCD的后缀数组
C[n1-1] = a1[n1-1];
for (int i = n1 - 2; i >= 0; i--)
C[i] = __gcd(A[i + 1], a1[i]);
//用于遍历数组
for (int i = 0; i <= n1; i++) {
//显示变量以存储除数
int cur1;
//现在得到除数
if (i == 0)
cur1 = C[i + 1];
else if (i == n1 - 1)
cur1 = A[i - 1];
else
cur1 = __gcd(A[i - 1], C[i + 1]);
//的除数
if (a1[i] % cur1 != 0)
return cur1;
}
return 0;
}
//驱动程式码
int main(){
int a1[] = { 50,15,40,41 };
int n1 = sizeof(a1) / sizeof(a1[0]);
cout << getDivisor1(a1, n1);
return 0;
}
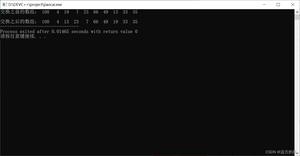
输出结果
5
以上是 查找一个整数X,该整数除C中数组中仅一个元素外的所有元素的除数 的全部内容, 来源链接: utcz.com/z/330911.html