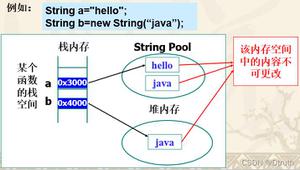
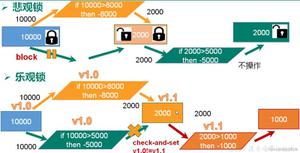
Java 最优二叉树的哈夫曼算法的简单实现
最优二叉树也称哈夫曼树,讲的直白点就是每个结点都带权值,我们让大的值离根近、小的值离根远,实现整体权值(带权路径长度)最小化。
哈夫曼算法的思想我认为就是上面讲的,而它的算法实现思路是这样的:
从根结点中抽出权值最小的两个(涉及排序,但是我这个实现代码没做严格的排序,只有比较)合并出新的根结点重新加入排序(被抽出来的两个自然是变成非根结点了啊),就这样循环下去,直到合并完成,我们得到一颗最优二叉树——哈夫曼树。
说明:
(1)哈夫曼树有n个叶子结点,则我们可以推出其有n-1个分支结点。因此我在定义名为huffmanTree的HuffmanNode类型数组时定义长度为2*n-1。
(2)这里排序相关没有做得很好,只是为了实现而实现,以后慢慢完善。
(3)理论上讲哈夫曼树应该是不仅仅局限于数值,能compare就行,但这里只用int表示。
下面是代码:
首先定义哈夫曼树结点
public class HuffmanNode {
private int weight = -1;
private int parent = -1;
private int left = -1;
private int right = -1;
public HuffmanNode(int weight) {
super();
this.weight = weight;
}
public HuffmanNode(int weight, int left, int right) {
super();
this.weight = weight;
this.left = left;
this.right = right;
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
public int getParent() {
return parent;
}
public void setParent(int parent) {
this.parent = parent;
}
public int getLeft() {
return left;
}
public void setLeft(int left) {
this.left = left;
}
public int getRight() {
return right;
}
public void setRight(int right) {
this.right = right;
}
@Override
public String toString() {
return "HuffmanNode [weight=" + weight + ", parent=" + parent + ","
+ " left=" + left + ", right=" + right + "]";
}
}
定义一下哈夫曼树的异常类
public class TreeException extends RuntimeException {
private static final long serialVersionUID = 1L;
public TreeException() {}
public TreeException(String message) {
super(message);
}
}
编码实现(做的处理不是那么高效)
public class HuffmanTree {
protected HuffmanNode[] huffmanTree;
public HuffmanTree(int[] leafs) {
//异常条件判断
if (leafs.length <= 1) {
throw new TreeException("叶子结点个数小于2,无法构建哈夫曼树");
}
//初始化储存空间
huffmanTree = new HuffmanNode[leafs.length*2-1];
//构造n棵只含根结点的二叉树
for (int i = 0; i < leafs.length; i++) {
HuffmanNode node = new HuffmanNode(leafs[i]);
huffmanTree[i] = node;
}
//构造哈夫曼树的选取与合并
for (int i = leafs.length; i < huffmanTree.length; i++) {
//获取权值最小的结点下标
int miniNum_1 = selectMiniNum1();
//获取权值次小的结点下标
int miniNum_2 = selectMiniNum2();
if (miniNum_1 == -1 || miniNum_2 == -1) {
return;
}
//两个权值最小的结点合并为新节点
HuffmanNode node = new HuffmanNode(huffmanTree[miniNum_1].getWeight() +
huffmanTree[miniNum_2].getWeight(), miniNum_1, miniNum_2);
huffmanTree[i] = node;
huffmanTree[miniNum_1].setParent(i);
huffmanTree[miniNum_2].setParent(i);
}
}
/**
* 获取权值最小的结点下标
* @return
*/
private int selectMiniNum1() {
//最小值
int min = -1;
//最小值下标
int index = -1;
//是否完成最小值初始化
boolean flag = false;
//遍历一遍
for (int i = 0; i < huffmanTree.length; i++) {
//排空、只看根结点,否则跳过
if (huffmanTree[i] == null || huffmanTree[i].getParent() != -1) {
continue;
} else if (!flag) { //没初始化先初始化然后跳过
//初始化
min = huffmanTree[i].getWeight();
index = i;
//以后不再初始化min
flag = true;
//跳过本次循环
continue;
}
int tempWeight = huffmanTree[i].getWeight();
//低效比较
if (tempWeight < min) {
min = tempWeight;
index = i;
}
}
return index;
}
/**
* 获取权值次小的结点下标
* @return
*/
private int selectMiniNum2() {
//次小值
int min = -1;
//是否完成次小值初始化
boolean flag = false;
//最小值下标(调用上面的方法)
int index = selectMiniNum1();
//最小值都不存在,则次小值也不存在
if (index == -1) {
return -1;
}
//次小值下标
int index2 = -1;
//遍历一遍
for (int i = 0; i < huffmanTree.length; i++) {
//最小值不要、排空、只看根结点,否则跳过
if (index == i || huffmanTree[i] == null || huffmanTree[i].getParent() != -1) {
continue;
} else if (!flag) { //没初始化先初始化然后跳过
//初始化
min = huffmanTree[i].getWeight();
index2 = i;
//以后不再初始化min
flag = true;
//跳过本次循环
continue;
}
int tempWeight = huffmanTree[i].getWeight();
//低效比较
if (tempWeight < min) {
min = tempWeight;
index2 = i;
}
}
return index2;
}
}
测试类1
public class HuffmanTreeTester {
public static void main(String[] args) {
int[] leafs = {1, 3, 5, 6, 2, 22, 77, 4, 9};
HuffmanTree tree = new HuffmanTree(leafs);
HuffmanNode[] nodeList = tree.huffmanTree;
for (HuffmanNode node : nodeList) {
System.out.println(node);
}
}
}
测试结果1
HuffmanNode [weight=1, parent=9, left=-1, right=-1]
HuffmanNode [weight=3, parent=10, left=-1, right=-1]
HuffmanNode [weight=5, parent=11, left=-1, right=-1]
HuffmanNode [weight=6, parent=12, left=-1, right=-1]
HuffmanNode [weight=2, parent=9, left=-1, right=-1]
HuffmanNode [weight=22, parent=15, left=-1, right=-1]
HuffmanNode [weight=77, parent=16, left=-1, right=-1]
HuffmanNode [weight=4, parent=11, left=-1, right=-1]
HuffmanNode [weight=9, parent=13, left=-1, right=-1]
HuffmanNode [weight=3, parent=10, left=0, right=4]
HuffmanNode [weight=6, parent=12, left=1, right=9]
HuffmanNode [weight=9, parent=13, left=7, right=2]
HuffmanNode [weight=12, parent=14, left=3, right=10]
HuffmanNode [weight=18, parent=14, left=8, right=11]
HuffmanNode [weight=30, parent=15, left=12, right=13]
HuffmanNode [weight=52, parent=16, left=5, right=14]
HuffmanNode [weight=129, parent=-1, left=15, right=6]
图形表示:
测试类2
public class HuffmanTreeTester {
public static void main(String[] args) {
int[] leafs = {2, 4, 5, 3};
HuffmanTree tree = new HuffmanTree(leafs);
HuffmanNode[] nodeList = tree.huffmanTree;
for (HuffmanNode node : nodeList) {
System.out.println(node);
}
}
}
测试结果2
HuffmanNode [weight=2, parent=4, left=-1, right=-1]
HuffmanNode [weight=4, parent=5, left=-1, right=-1]
HuffmanNode [weight=5, parent=5, left=-1, right=-1]
HuffmanNode [weight=3, parent=4, left=-1, right=-1]
HuffmanNode [weight=5, parent=6, left=0, right=3]
HuffmanNode [weight=9, parent=6, left=1, right=2]
HuffmanNode [weight=14, parent=-1, left=4, right=5]
图形表示:
以上是 Java 最优二叉树的哈夫曼算法的简单实现 的全部内容, 来源链接: utcz.com/z/312380.html