我对Paxos算法的理解
在分布式系统中,一个核心的问题就是数据的一致性。因此一致性算法是分布式中的重中之重。Paxos算法就是为了很好的解决一致性的问题,但是一直以来它都被认为是很难理解的,可能是因为它是用平常的语言来描述的,所以对于读者来说很难理解。想要了解Paxos算法,建议还是先好好的拜读一下“原著”——《Paxos Made Simple》。
好了,废话不多说,下面开始走进Paxos的世界。
问题的提出
假定有一组程序要提交一些值,那如何保证这些值的唯一性呢?一致性算法就是来保证这些值中只有一个值被选定。当然了,如果一个值被选定了,那么这些程序应该能获得这个被选定的值。
因此,我们看到,在这一个过程中应该包含三种角色——proposers(提议者)、acceptors和learners。在这个实现这个算法的过程中一个成员可能要扮演多个角色。
选择一个值得最简单的方式就是使各组成员中只有一个acceptor,一个proposer向这个acceptor提交提案,该acceptor选择它接收到的第一个提案。这种方式虽然简单,但是并不能满足我们的要求。因为,一旦这个acceptor出现问题,则该程序将是没有办法继续走下去的。
因此,这里需要我们使用其他的方法来选择这个值了。我们不使用单个的acceptor,取而代之的是我们使用多个acceptor来完成这个过程。也就是说proposer从之前的向一个acceptor提交提案改成向一组acceptor提交提案。一个acceptor会批准一个提案。一个提案的值被一个足够大的组中的所有acceptor所批准,就说该提案被选中了。那问题来了,多大的组才算是足够大呢[Q1]?
对于Q1,我们可以这样来理解:对于所有的acceptor有集合{acceptor1 , acceptor2 , acceptor3 , .. , acceptor(n)} A。假设有一个集合T,T中的每个元素都是一组acceptor。T中的这些组都是由A中的acceptor所组成的。
T:{{acceptor(k),acceptor(k+1), ...,acceptor(j)}, {acceptor1,acceptor2,...,acceptor(m)}, ..., {acceptor(l),acceptor(l+1),...,acceptor(n)}}
对于T中的任意两组acceptor至少有一个公共acceptor。这样的集合T就可以被认为是足够大的,也就是在Q1中提出的足够大的组。
好,清楚了这个足够大的组以后我们继续向下走。因为任意两个组至少有一个公共acceptor,所以说只有在一个acceptor最多只批准一个提案的情况下才能够选定一个提案。这里需要说明一下,一个acceptor最多只批准一个提案是在一次选举的过程中。当进行下一次选举的时候是被允许再次批准提案的。说到这里大家对这个问题可能有些模糊。没关系,请继续往下看,理解了后面的问题在回到这里看就豁然开朗了。
在没有信息丢失的情况下,即使只有一个proposer提交了一个提案,我们也是希望该提案被选中的。这样就产生了Paxos算法中的第一个条件:
P1. 一个acceptor必须批准它接收到的第一个提案。
在原著中是这样说的:
P1. An acceptor must accept the first proposal that it recevies.
这里我翻译的应该没有错。
但是,我们看,对于P1的要求应该会产生这样的一个问题。当多个proposer在同一时间内提交了多个不同的提案,这是有可能会出现没有一个提案会被多数以上的acceptor所批准[Q2]。关于这个问题该怎么来理解呢?在P1的要求下——每个acceptor必须批准它接收到的第一个提案。所以会出现下面的情景:
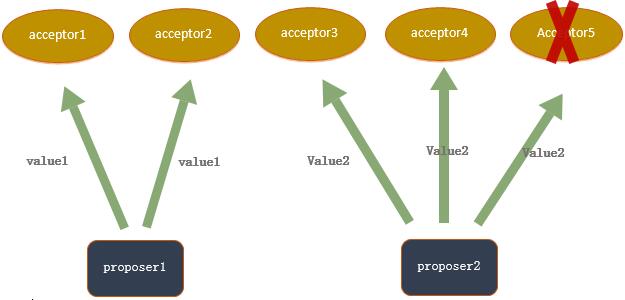
多个acceptor接收到的提案都不相同
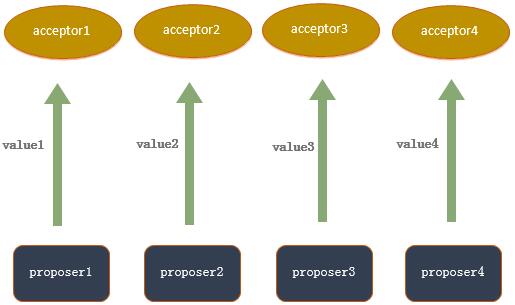
也就是说acceptor1第一个接收到value1,acceptor2第一个接收到value2,... 以此类推。他们都批准接收到的第一个提案,所以就导致了Q2中产生的问题。即使说只有两个提案被提出,并且每个提案都被差不多一半的acceptor所批准,即使只有一个acceptor出错,也没有办法保证在P1的要求下有一个提案被选定。
我们知道,一个提案被选中的前提是该提案被一半以上的acceptor所批准。而在P1中又规定,一个acceptor必须批准它接收到的第一个提案,所以从P1条件又产生了我们上面所解释的问题Q2。所以综合上面的情况,我们可以推导出一个acceptor必须被允许接收多个提案。acceptor会为每个提案分配一个序号。那么到这个地方我们的提案就已经更换了,不再是只有value构成,现在的提案是由编号和value两部分构成。同时要求任何两个提案之间的编号都不相同。到目前为止,我们又有了两个武器:
1. 一个acceptor可以接收多个提案。
2. 每个提案由编号和value两部分共同组成。任意的两个提案的编号都不相同。
拿起我们的武器继续前进。接下来有两个结论需要说明一下。
一个提案要想被选中,必须被一半以上的acceptor所批准;我们允许再一次选举过程中有多个提案被选中,但是这些被选中的提案的value值必须相同。到这里好像能见到一丝光明了。提案有了编号,这就给我们后续的论证有了很大的帮助。在算法中只要能够保证下面的条件成立,我们就能保证选中的提案的唯一性:
P2:如果一个带有v的提案被选中了,假设该提案的编号为m。那么任何大于m的被选中的提案的值都为v。
同样P2在原著中是这样说的
P2:If a proposal wiht value v is chosen, then every higher-numbered proposal that is chosen has value v.
因为编号是有序的。所以说能保证P2成立的话,就能满足我们最初的要求。
不过看了P2就感觉先前看到的那一丝光明又消失了。且看P1是要每个acceptor批准其接收到的第一个提案。而到了P2则讨论的就直接是对于选中的提案的要求。从P1到P2这期间究竟发生了什么,我们不得而知。不过没关系,毕竟我们从P2中可以知道,只要满足了P2就能满足只有一个值被选中的这一关键点——这也是我们所希望达到的目的。
下面我们来做的就是反推应该如何来保证P2能够成立。说到这是不是刚才感觉要消失的那一丝光明又在眼前重现了。
那P2又该如何来满足呢?首先,一个提案要想被选中,那该提案必须被至少一个acceptor所批准。这一点是毋庸置疑的。因此,新的条件又产生了。
P2a:如果一个值为v的提案被选中了,假设编号为m。那么对于每个编号大于m的提案来说,如果被acceptor批准,该提案的值也必须为v。
该条件在原著中是这样说的
P2a: If a proposal whth value v is chosen, then every heigher-numbered proposal accepted by any acceptor has value v.
经过P2a,貌似P2可以得到满足了。因为提案的编号是全序的,也就是说后提交的提案的编号肯定是大于先提交的提案的编号了。而对于P2a条件中的要求,后提交的并且被批准的提案其值必须为v。这样P2肯定会被满足了。
所以说只要满足P2a就能满足P2从而我们最初的目的也能达到,至少目前是这样的。但是,我们再回过头来看P1,就会发现,其实还有一些地方是我们遗漏的。我们知道,成员之间的通信是异步的。假如有一个acceptor,暂称其为C,还未收到任何提案的时候有一个编号为m的提案就已经被选中了。假设这时一个新的proposer被唤醒,然后提交了一个编号大于m的提案,并且该提案的值和m也不相同。当C收到这个提案以后,根据P1,C是必须要批准这个提案的。这时就违背了P2a了。对于P2a,我们能看出,是站在acceptor角度提出的。因此就产生了上面的问题。所以需要再次站在proposer的角度来提出一些限制。
P2b: 一个值为v的提案被选定了,该提案编号为m。那么对于任何编号大于m的由proposer提交的提案的值必须为v。
同样我们引用原文
P2b: If a proposal with value v is chosen, then every higher-numbered proposal issued by any proposer has value v.
由于一个提案在被acceptor批准之前必须由提议者提交,因此P2b可以满足P2a从而满足了P2。在这里,站在proposer的角度提出了P2b。那又该如何来保证P2b呢?我们假设某个编号为m,值为v的提案被选中了,对于任何被提出的编号为 n(n > m)的提案,其值都为v。现在我们使用归纳法来证明该说法是成立的。
提案[ m , v ]被选中,我们的假设条件如下
对于编号在 m...(n-1) 中的任何一个被提出的提案的值都为v。
同时由于提案m被选中,因此肯定有一个集合C,包含半数以上的acceptor,C中的每一个acceptor都批准了提案m。因此我们可以推断出,在C中的每一个acceptor都批准了编号在m...(n-1)范围内的一个提案,并且m...(n-1)中的被任意一个acceptor批准的提案的值都为v(这里需要注意的是,任意一个acceptor并不都是值得C中的acceptor)。
由于任意一个集合S,包含了半数以上的acceptor,肯定会至少包含一个C中的acceptor,所以我们可以通过下面的条件来满足P2b。也就是任意一个被提出的编号为n (n > m)的提案的值都为v。
P2c:对于任意的v和n,如果一个编号为n,值为v的提案被提出的话,肯定存在一个包含半数以上的acceptor的集合S满足:要么集合S中没有一个acceptor批准过任意的编号小于n的提案;要么对于集合S中批准的编号小于n的那些提案中,编号最大的提案的值为v。
通过保持P2c的不变性,就能保证P2b。从而满足P2a,进而满足P2。最终满足我们最初的要求。
同样的,问题又来了。既然由P2c => P2b => P2a => P2。那我们又由什么来证明P2c的完整性呢[Q3]?
对于Q3,我们可以使用反证法来证明。
假设提案[m,v]已经被选定,有提案n ① n=m+1 假设n的值不为v,而为w。则根据P2c要么有一组S从来没有批准过小于n的提案;要么在批准的所有编号小于n的提案中,编号最大的提案的值为w。因为S和C至少有一个公共acceptor,所以说两个条件都不满足。所以假设不成立。因此n的值为v。② 编号m属于m...(n-1),假设n的值不为v,设为w’ 。则存在一个集合S’,要么在S’中没有一个acceptor批准过编号小于n的提案;要么在S’中批准过的所有的编号小于n的提案中,编号最大的提案的值为w’,设该提案的编号为p(p∈m...(n-1))。根据我们在归纳法中的假设条件编号属于m...(n-1)的提案的值都为v,并且S’和C至少有一个公共acceptor,所以由S’中的acceptor批准的小于n的提案中编号最大的那个提案也属于m...(n-1)。从而可以推导出w’=v。即可证明提案n的值为v。
到这里我们就证明了P2C的完整性。
由此可见,一个proposer要想提交一个编号为n的提案,首先获取到编号小于n的那些提案中编号最大的那个提案,假设该提案编号为p,如果有这个提案的话,提案p已经或者将要被某一个包含半数以上的acceptor的集合中的所有的acceptor所批准。获取这样的一个已经被批准的提案是非常简单的,相反预测一个批准的提案是非常困难的。所以,一个proposer可以请求acceptor不要批准任何小于编号n的提案。这时,核心的算法就要产生了:
1. 一个proposer准备提交一个编号为n的提案之前,首先会向某组(含半数以上的acceptor)中的每个成员发出请求,希望得到如下的响应:
a. Acceptor承诺不再批准任何编号小于n的提案。
b. 如果acceptor批准过小于编号n的提案,则将编号最大的提案响应给proposer。
我们称这个请求过程为提案n的prepare请求。
2. 如果proposer从某个组(包含半数以上的acceptor)中的acceptor方面得到响应,那么该proposer就可以提交值为v的提案n了。当然了,这里的v要视响应消息而定。如果得到的响应是acceptor已经批准的编号小于n的的那些提案中的编号最大的提案,那么提案n的值v就是响应的提案的值;如果得到的响应消息是acceptor没有批准过任何编号小于n的提案,那么值v就可以是任意的了。得到prepare请求的响应以后,proposer再次向同一
acceptor发出批准该提案的请求。我们称其为accept请求。
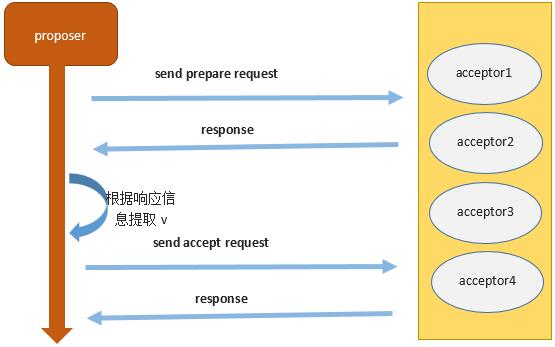
上面的算法是对proposer提出的。那对于acceptor方面有该如何处理呢?在上面的过程中,acceptor会收到两种类型的请求:prepare和accept。
acceptor是可以忽略任何请求的,并且不用考虑是否能满足什么条件。 所以说,这里我们说的是acceptor会对一个请求进行响应的情况。acceptor对于prepare 请求总是会积极响应。对于accept请求,如果他没有响应过不去批准该提案,那它会响应一个批准该提案的消息。也就是下面的条件
P1a:acceptor对于编号为n的提案的accept请求,如果之前没有对编号大于n的提案的prepare请求进行过响应,那么该acceptor会批准编号为n的提案。
原著中是这样描述的
P1a. An acceptor can accept a proposal numbered n iff it has not responded to a prepare request having a number greater than n.
我们看,在P1a中是包含P1的。
到目前为止我们已经有了一个比较完整的算法。现在我们将proposer和acceptor综合起来,看一下整个算法的过程。
Phase1 (a)proposer选择一个编号为n的提案,并且发送一个带有编号n的prepare请求给一组包含半数以上的acceptor。
(b)一个acceptor接收到一个关于编号n的prepare请求,发现编号n比其先前接收到的所有的提案的编号都大,并且对于这些提案的prepare请求都已经进行了响应。那么acceptor会向n的prepare请求回应的消息包括两部分:一是,不会再批准任何小于n的提案;二是,将已经批准的编号小于n的的那些提案中的编号最大的提案的值,当然这个提案要存在。如果不存在则仅仅响应第一条。
Phase2 (a)当proposer从包含半数以上的一组acceptor那里收到关于编号n的提案的prepare请求的响应信息,那么它将会向这组acceptor发送一个编号为n值为v的提案的accept请求。这个v的值根据proposer得到的响应信息来定:如果在响应信息中包含有提案信息,那这个v就是该提案的值;如果没有提案信息,则v可以是任意值,只要proposer愿意。
(b)如果acceptor收到一个关于n的提案的accept请求,除非acceptor已经向大于n的提案的prepare请求进行了响应,否则该acceptor是会批准编号为n的提案的。
一个proposer只要遵循上面的步骤,他就可以生成多个提案。在上面的过程中,proposer可以在任意的时刻终止一个提案。对于acceptor来说,无论如何,如果acceptor由于之前已经向一个编号更大的提案的prepare请求进行了响应而要忽略当前提案的prepare或者accept请求的话,必须要能通知到proposer。由proposer来放弃这个提案的提交。
上面就是关于proposer和acceptor的算法。说到这里,对于proposer和acceptor要做的事情就已经清楚了。但是我们知道,在Paxos算法中是存在三种角色的。除了proposer和acceptor以外还有learner。既然我们的提案已经选出来了,那就需要learner来学习了。下面我们就来看一下learner是如何学习一个已经被选中的提案的。
最简单的方式就是,learner必须获取被半数以上acceptor批准的提案。所以,必须使每个acceptor,不论何时只要它批准一个提案就会通知到所有的learner,并将批准的proposal发送给learner。因此,learner可以及时的获取一个被选中的提案。但是,这种方式的代价就是会有大量的通信。因为这种方式要求每个acceptor向每个learner都要发送消息。[方式一]
还有一个方式就是,指定一个特定的learner负责和acceptor进行通信。acceptor只负责将其批准的提案发送给这个特定的learner,由这个learner再将其发送给其他的learner。[方式二]
方式二虽然有效的减少、了通信的次数,但是这种方式却是不可靠的。因为一旦那个特定的learner出现故障,所有的learner都将获取不到提案。所以在方式二的基础上演变出来了方式三。不再指定一个特定的learner,而是指定多个learner负责和acceptor通信,然后再将信息发送给其他的learner。很明显,这种方式较方式二来说通信次数又增加了,但是较方式一,通信次数依然是减少的。而且这种方式是比较可靠的。
考虑到,在实际场景中消息是会丢失的。一个被选中的提案可能不会被learner获取到。这时候它可以向acceptor询问一个其已经批准的提案,但是这个acceptor是没有办法知道这个提案是否被大多数的acceptor所批准。在这种情况下,learner可以求助于proposer。它可以让一个proposer按照之前描述的步骤来提交一个提案。如果该提案被提交成功了,根据之前的P2c、P2b等条件可以知道该提案的值已经被选中;否则该值没有被选中。
算法到这里就已经完整了。对于开始说到的三个角色——proposer、acceptor和learner,各自要进行的动作都已经明确了。下面来说一个比较特殊的情况。
我们来假设这样的一个情景:有两个proposer——p和q,每一个都会提出一系列编号递增的提案。这些提案都没有别选中过。现在p完成了阶段1的编号为n1的提案。然后p完成了阶段1的编号为n2(n2 > n1)的提案。所以对于n1的阶段2的accept请求会被忽略,因为所有的acceptor都已经向n2的prepare响应了不会再批准任何编号小于n2的提案。因此,p开始提出n3(n3 > n2),并且完成了prepare的请求。同样,这时n2的accept请求也会被忽略。以此进行下去岂不是就成了一个死循环了。
为了解决这个问题,参照learner学习提案的方式二,指定一个特定的proposer,使其作为唯一的可以提出提案的proposer。
所有上面的算法都有一个前提,就是任何两个proposer提出的提案的编号都不相同。
上面一堆堆的文字可能有些啰嗦,多数都是参照原文翻译过来的。有不确切的地方还希望多多指教!
参考文献:《Paxos Made Simple》
本文转载自:迹忆客(https://www.jiyik.com)
以上是 我对Paxos算法的理解 的全部内容, 来源链接: utcz.com/z/290143.html