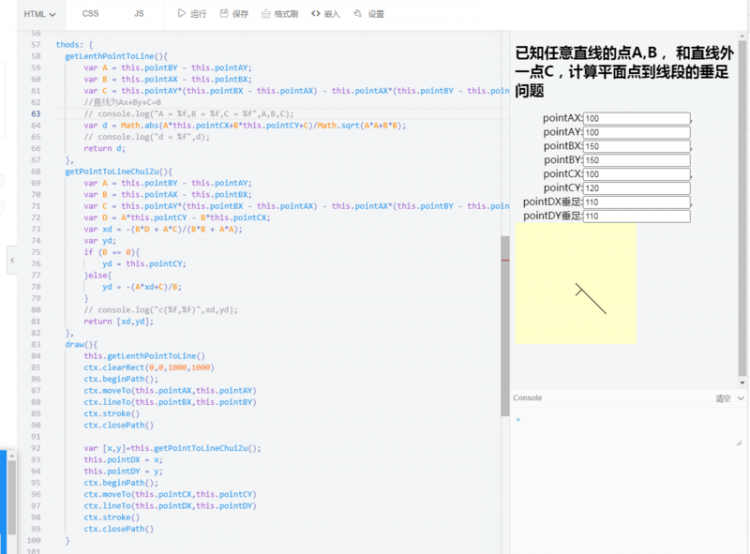
计算平面点到线段的垂足问题

• Z时代
• 2024-01-10
• 分类：技术分享

如图，以左上为原点的坐标图，坐标都为正

已知任意直线的点A,B， 和直线外一点C
目前用向量法还是直线方程的方法，然后都有偏移的情况 。
向量法结果在A点，直线方程结果在CB线上。
(另外线AB方向是不确定的，可能是AB也可能是BA, 可能是各种方向上)

现在的方法有时是正常的，有时是错误的， 图上是错误时的用例

向量法

// 求垂足座标, C(x0,y0), A(x1, y1) B(x2, y2)
func VerticalAix(x0, y0, x1, y1, x2, y2 int) (int, int) {
dx := x1 - x2
dy := y1 - y2
if math.Abs(float64(dx)) < 0.00000001 && math.Abs(float64(dy)) < 0.00000001 {
return x0, y0
}
u := (x0-x1)*(x1-x2) +
(y0-y1)*(y1-y2)
u = u / ((dx * dx) + (dy * dy))
x := x1 + u*dx
y := y1 + u*dy
return x, y
}

直线方程

// 求垂足座标  C(x0,y0), A(x1, y1) B(x2, y2)
func VerticalAix(x0, y0, x1, y1, x2, y2 int) (int, int) {
if x2-x1 == 0 {
return x2, y0
}
// 算斜率
k1 := (y2 - y1) / (x2 - x1)
// 垂足x坐标
x := (math.Pow(float64(k1), 2)*float64(x1) + float64(k1*(y0-y1)) + float64(x0)) / (math.Pow(float64(k1), 2) + 1)
y := float64(k1)*(x-float64(x1)) + float64(y1)
return int(x), int(y)
}

https://play.golang.org/p/WFy...

回答

//点P到线段AB的距离
//使用矢量算法，计算线AP在线段AB方向上的投影
function PointToSegDist(point, point1, point2){
  let x = point[0], x1 = point1[0], x2 = point2[0]
  let y = point[1], y1 = point1[1], y2 = point2[1]
  let cross = (x2 - x1) * (x - x1) + (y2 - y1) * (y - y1);
  let d2 = (x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1);
  //r = 0 垂足为point1  r = 1 垂足为point2
  let r = cross / d2;
  let px = x1 + (x2 - x1) * r;
  let py = y1 + (y2 - y1) * r;
  return {
    type: r >= 0 && r <= 1, //true  垂足在线段内   false 垂足在线段外
    point: [px, py],
    dist: Math.sqrt((x - px) * (x - px) + (py - y) * (py - y))
  };
}
PointToSegDist([1520, 8026], [1306, 8000], [2940, 6863]); 
//{ type: true, dist: 143.57151930446304, point: [1437.9966124321018, 7908.151684005325] }

http://jsrun.net/MaIKp/edit

从网上随便找了个公式套了进去，看上去是没问题的

以上是 计算平面点到线段的垂足问题 的全部内容， 来源链接： utcz.com/a/79590.html