Extraction of the Quad Layout of a Triangle Mesh Guided by Its Curve Skeleton

简介

论文简单构述了一个主题，输入三角网格，根据三角网格的骨架信息得到四边形网格

流程步骤

Extraction of the Quad Layout of a Triangle Mesh Guided by Its Curve Skeleton

TIPS:

注意红色节点是分支节点和边节点，但是之间其实还是有一部分的折线，逻辑上也是一种节点。这种节点采用的直线的切平面构建的“四边形部分”；

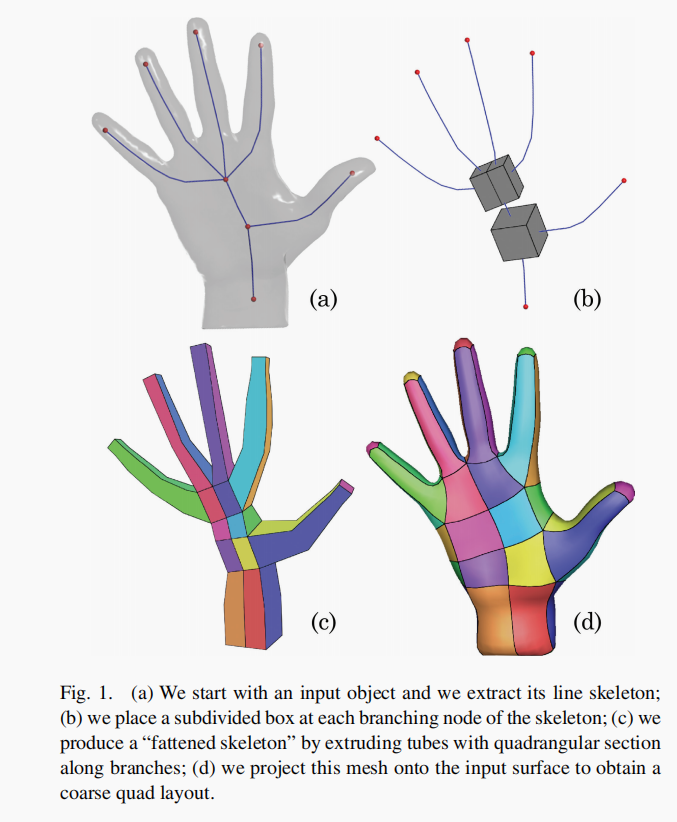
Step 1: 输入三角网格，我们提取他的骨架结构信息
Step 2: 我们放置了一个细分盒子在每一个分支节点处。
Step 3: 我们在沿着管道(分支节点和分支节点,分支节点和边节点）在每个转折处放置一个四边形的面构成一个管道盒子（四边形部分）
Step 4: 我们投影这个网格到输入表面去获得一个粗糙的四边形输出

不足：不能构造精细的网格

作者回顾前人的做法，发现前人没有关于生成粗四边形网格的做法。

奇异点会在分支节点出产生。

基本步骤，生成分支节点六面体，使用整数线性规划方法来调整六面体的站位。

生成六面体。然后参数化将生成的面投影得到原来的面上得到四边形网格。

\[\left\{

\begin{aligned}

Jn & = & 2 vector \\

En & = & 1 vector \\

Bn & = & >= 2 vector

\end{aligned}

\right.

\]

ILP (整数线性规划问题)

对于一个cubic(立方体)输入的向量\({d_1^i,...d_{k_i}^i}\)，我们搜索三个相互垂直的向量\(U_i V_i W_i\)让下面的方程有最下滑的值。

\[f(U_i, V_i, W_i) = \sum^{k_i}_{j=1} |d^i_j \cdot U_i| + |d^i_j \cdot V_i| + |d_j^i \cdot W_i|.

\]

因为绝对值很难进行优化，作者采用了Huang在2014年提出的论文，最小化函数当\(\epsilon \rightarrow 0\)

\[f_{\epsilon}(U_i, V_i, W_i) = \sum^{k_i}_{j=1} \sqrt{(d^i_j \cdot U_i)^2 + \epsilon} + \sqrt{(d^i_j \cdot V_i)^2 + \epsilon} + \sqrt{(d_j^i \cdot W_i)^2 + \epsilon}

\]

以上是 Extraction of the Quad Layout of a Triangle Mesh Guided by Its Curve Skeleton 的全部内容， 来源链接： utcz.com/a/74165.html

回到顶部