🔢【程序中的数学】利用德摩根定律简化布尔运算

今天说说德摩根定律在编程中的实践，题目看的很吓人，其实只要有一点点的高中数学知识就能看懂，而且这部分知识掌握后可以很快的运用到项目中，投资收益比非常高。

如果你觉得我的文章对你有帮助，在收藏的过程中，一定要记得点赞哦，谢谢你，这对我真的很重要🌟！

一、缘起：一段让人头大的逻辑判断

这两天在重构一些老项目，重构过程中遇到了一个让人非常头大的逻辑判断：

if(!((A && B) || C)) {
// do something
} else {
// do something
}

看了这段代码，我人都傻了，从里向外一层一层梳理逻辑时，我的大脑活动是这样的：

🔢【程序中的数学】利用德摩根定律简化布尔运算

短短一行的逻辑判断里，与或非三个运算符都用上了，尤其是最后那个小括号一圈全体取反的操作，我脑子直接炸了。要知道人脑是很不擅长或运算和非运算的，更不要说这些运算组合在一起了。

又花了五分钟尝试从代码上下文中梳理业务逻辑无果后，我重新审视了这个问题：如果业务上不好处理这个问题，能不能从理论上找到突破口？

方向找对后，我很快就找到了解决方案，那就是离散数学里的德摩根定律（De Morgan's laws）。

二、什么是德摩根定律

德摩根定律我们其实很早就接触过了，高中数学的集合部分就讲过，大学离散数学的集合运算和布尔代数部分也有所提及。

德摩根定律在离散数学的很多场景里都出现过，它一共有两个关系：

  • 在命题逻辑里，可以这样表示：

$$\neg (P\lor Q)\iff (\neg P)\land (\neg Q)$$

$$\neg (P\land Q)\iff (\neg P)\lor (\neg Q)$$

其中 $\neg$ 表示逻辑非运算符（NOT, !），$\lor$ 表示逻辑或运算符（OR, ||），$\land$ 表示逻辑与运算符（AND, &&）


  • 在集合里可以这样表示：

$$\overline {A\cup B} = \overline {A} \cap \overline {B}$$

$$\overline {A\cap B} = \overline {A} \cup \overline {B}$$

其中 A 和 B 表示集合，集合上的横线表示取补集，$\cap$ 表示取交集，$\cup$ 表示取并集。


  • 在布尔代数里可以这样表示：

$$\overline {(x \cdot y)} = \overline {x} + \overline {y}$$

$$\overline {(x+y)} = \overline {x} \cdot \overline {y}$$

其中 $\cdot$ 表示布尔积（AND），$+$ 表示布尔和（OR），上划线表示补（NOT）。


  • 上面的公式还可以用文字描述：

非（$P$ 或 $Q$）等价于（非 $P$）且（非 $Q$）

非（$P$ 且 $Q$）等价于（非 $P$）或（非 $Q$）


  • 或者用程序员熟悉的与或非逻辑运算符表示：

!(P || Q) = !P && !Q
!(P && Q) = !P || !Q

公式已经摆在这里了，肯定可以直接用了，但是用的时候还是不太放心，最好还是自己验证一下。我们可以用真值表对 $\neg (P\land Q)\iff (\neg P)\lor (\neg Q)$ 做个直观的验证：

$P$$Q$$\neg P$$\neg Q$$(P\land Q)$$\neg (P\land Q)$$(\neg P)\lor (\neg Q)$
0011011
0110011
1001011
1100100

我们也可以用 Venn 图对 $\overline {A\cap B} = \overline {A} \cup \overline {B}$ 做个可视化验证：

🔢【程序中的数学】利用德摩根定律简化布尔运算

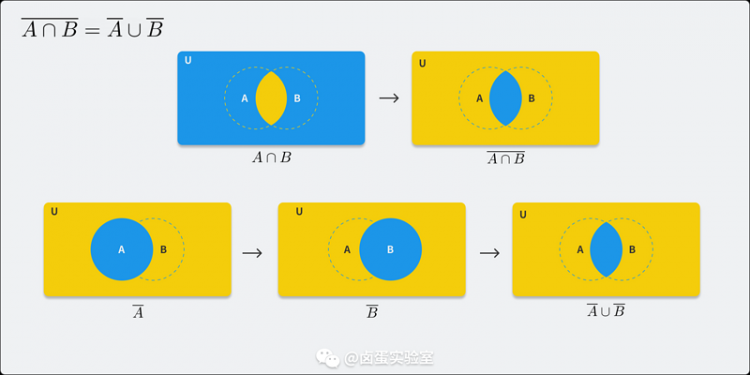
更复杂的数学推导我这里就不多说了，感兴趣的同学可以自行搜索学习。

三、解决问题

具体到我一开始说的那个条件判断上，我们可以用德摩根定律把原表达式拆开：

!((A && B) || C)
== !(A && B) && !C   // 德摩根律
== (!A || !B) && !C  // 德摩根律
== (!A && !C) || (!B && !C)  // 分配律

用分配律转化后，经过代码的上下文分析，我发现在这段代码的业务场景中， !A 等价于 C，所以上面的式子还可以化简：

(!A && !C) || (!B && !C)
== (C && !C) || (!B && !C) // !A 等价于 C（从业务上分析的，不具备普遍意义）
== false || (!B && !C)     // C && !C 必定为 false
== !B && !C
== A && !B  // A 等价于 !C（从业务上分析的）

到这里，我成功的把原来一段让人脑袋爆炸的判断语句化简为一段直白易懂的表达式，转换后的代码无论是从理解上还是后期维护上都比原来容易很多。

四、化简还有什么招？

与或非三者一起用的场景可以尝试用德摩根定律化简，在其它场景下，还可以利用其它运算律进行转换，比如说前面我就用了分配律。类似于积之和展开式的化简，我们还可以用卡诺图进行分析。

例如一个场景试图化简布尔函数的一个积之展开式：$x\overline {y} + \overline {x}y + \overline {x} \overline {y}$ ，就可以用卡诺图进行分析：

$y$$\overline {y}$
$x$1
$\overline {x}$11

根据图示可以轻易得出最后的化简结果为 $\overline {x} + \overline {y}$。

如果变量超过 4 个，卡诺图就非常复杂了，这时候可以用奎因-莫克拉斯基方法进行化简，限于篇幅也不多介绍了，感兴趣的同学可以自行搜索。

在此我再多说一句，如果真的出现用 4 个以上的子状态去决定最终的行为时，问题的关键就不是化简，而是顶层设计上就出了问题了。这时候需要停下来好好思考是不是模型的设计抽象程度不够，把过多的内部状态暴露了出来等等，这个得具体业务具体分析，一昧的堆 if else 或加 flag 是解决不了问题的，只会导致代码的腐化最终无法维护。

最后推荐一波我的微信公众号：卤蛋实验室和我的个人博客：supercodepower.com, 目前专注前端技术，对图形学也有一些微小研究，欢迎大家来撩～

五、推荐阅读

【答疑解惑】为什么你的 Charles 会抓包失败？

webpack 中那些最易混淆的 5 个知识点

React Native 性能优化指南【全网最全，值得收藏】

以上是 🔢【程序中的数学】利用德摩根定律简化布尔运算 的全部内容， 来源链接： utcz.com/a/62221.html

回到顶部