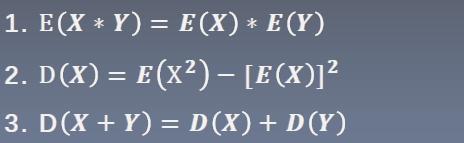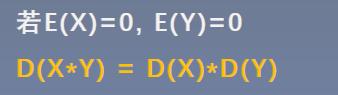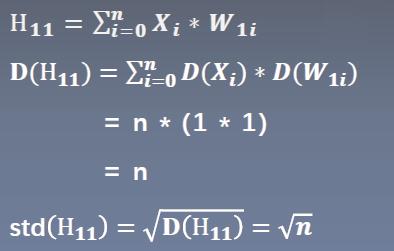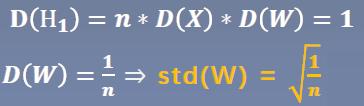5.4 权值初始化

前面学习了如何搭建网络模型。在模型搭建好之后，一个很重要的步骤就是对模型进行初始化。

正确的取值初始化可以加快模型的收敛，不恰当的模型初始化可能引发梯度的消失或爆炸，最终导致模型无法训练。

一、模型初始化不恰当可能引起梯度消失或爆炸

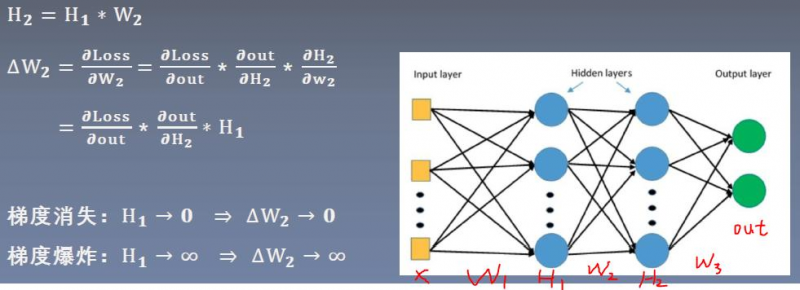
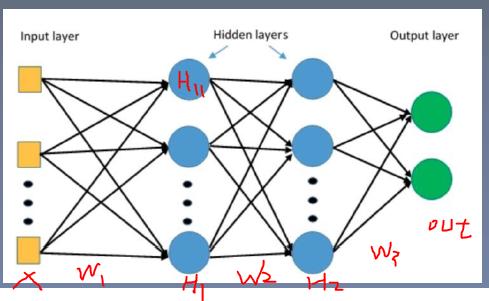
我们使用右边的模型：

观察w2的梯度是怎么来的。

求w2的梯度时，需要用到H1。如果H1的值非常小，那么w2的梯度也会很小，从而导致梯度消失；如果H1的值非常大，那么w2的梯度也会很大，从而导致梯度爆炸。一旦发生梯度消失或爆炸，会导致模型无法训练。

从公式推导可以看出，要避免梯度消失或爆炸，要严格控制网络输出层输出值的尺度的范围，不能太大或太小。

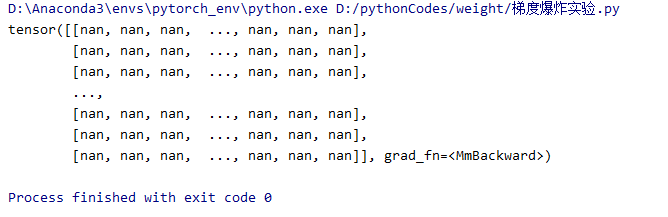
例：

# -*- coding: utf-8 -*-
"""
# @file name  : grad_vanish_explod.py
# @brief      : 梯度爆炸
"""
import os
BASE_DIR = os.path.dirname(os.path.abspath(__file__))
import torch
import random
import numpy as np
import torch.nn as nn
class MLP(nn.Module):
def __init__(self, neural_num, layers):
super(MLP, self).__init__()
self.linears = nn.ModuleList([nn.Linear(neural_num, neural_num, bias=False) for i in range(layers)])
self.neural_num = neural_num
def forward(self, x):
for (i, linear) in enumerate(self.linears):
x = linear(x)
return x
def initialize(self):
for m in self.modules():
if isinstance(m, nn.Linear):
nn.init.normal_(m.weight.data)  #normal:mean=0, std=1
layer_nums = 100
neural_nums = 256
batch_size = 16
net = MLP(neural_nums, layer_nums)
net.initialize()
inputs = torch.randn((batch_size, neural_nums))  # normal: mean=0, std=1
output = net(inputs)
print(output)

结果：

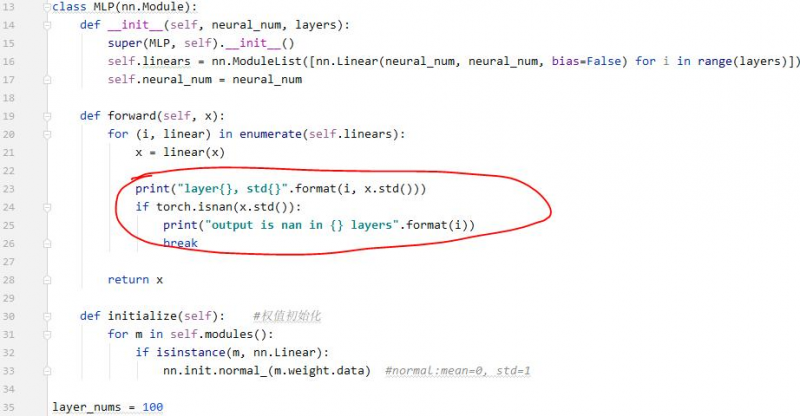
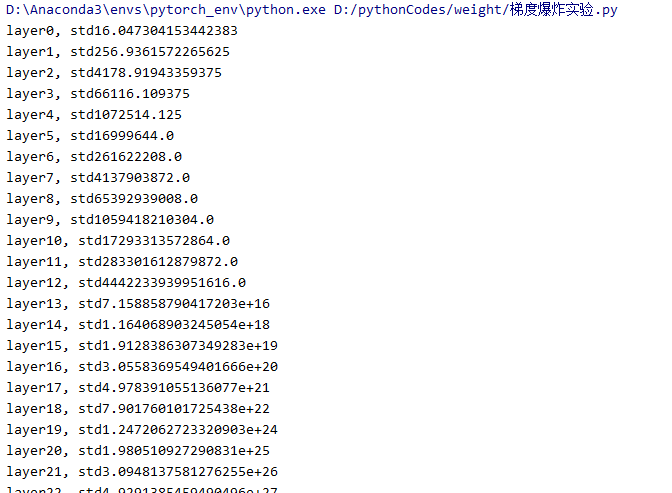
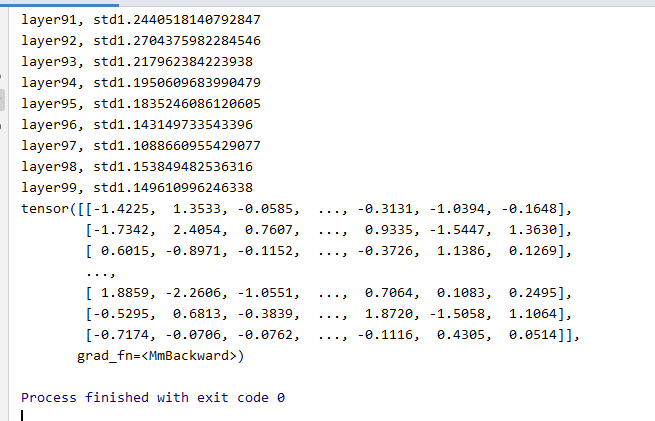
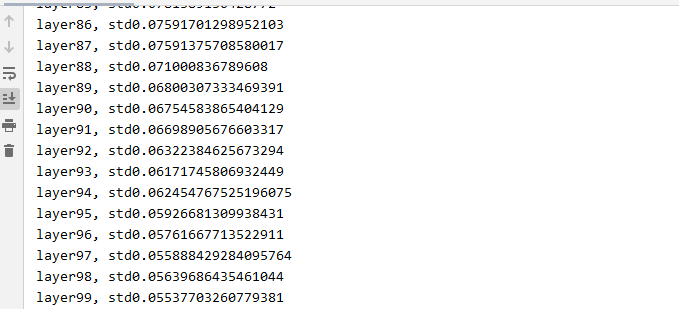
我们发现output的每一个值都是nan,也就是数值可能非常大或非常小，已经超出了当前精度可表示的范围。

现在我们到forward中观察一下什么时候数据变到了nan。我们把每一层的标准差打印出来。

也可以看到标准差越来越大。在第31层的时候，数据的标准差就已经是nan了。

下面我们通过方差的公式推导，来观察为什么网络的输出的标准差会越来越大，最终超出我们可表示的范围。

在进行方差公式推导之前，先复习3个基本公式：

1. 两个相互独立的随机变量，乘积的期望等于期望的乘积。

2. 方差的公式。

3. 两个相互独立的随机变量，和的方差等于方差的和。

通过以上3个公式，可以推导出：两个相互独立的随机变量乘积的方差为：

如果x、y的期望是0，则有：

如果x的均值为0，标准差为1。下面来观察H11的标准差是怎么样的。

由于Xi和W1i都是0均值，1标准差的。所以可以得到下面的公式：

也就是X的标准差是1，往后传播一层标准差变为了根号n。（看上面的代码的输出也可以看到这个规律）

同理传播到第二个隐藏层的时候，标准差会变为n。

不断往后传播，标准差会不断扩大。。。

从公式可以看到，标准差有三个因素影响。n、D(xi)、D(w1i)

如果想让网络层的方差保持尺度不变，那只能让方差等于1。（因为是进行多个数相乘，多个数相乘尺度不变的数只有1）

所以有：

因此，当权值的标准差设置为根号(1/n)时，每一个网络层输出的标准差都是1.

下面我们才用0均值，标准差是根号(1/n)的分布去初始化权值，再来观察网络层输出的标准差。

代码：

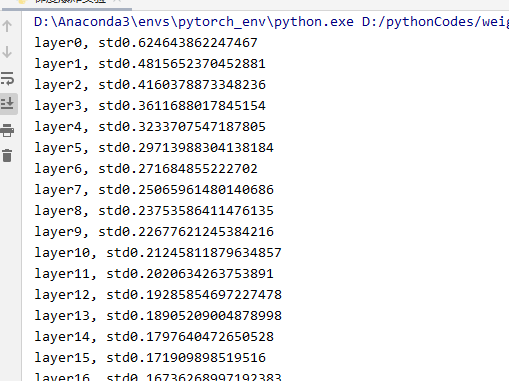
结果：

可以看到在100层的时候，输出的标准差都比较正常。

结论：我们才用恰当的权值初始化方法，可以实现多层的全连接网络的输出值的尺度维持在一定的范围之内。

通过以上的例子，我们知道需要保持每个网络层输出的方差是1。但是在这里我们还未考虑到激活函数的存在，下面我们来学习具有激活函数时的权值初始化。

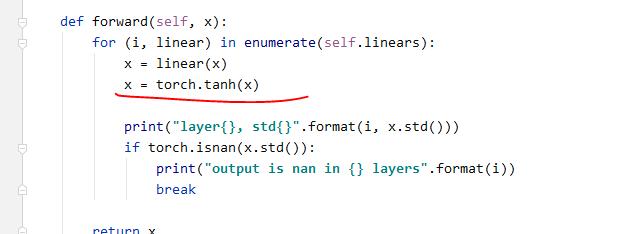
我们在每个线性变换后面加一个激活函数。看一下输出值的变化：

结果：

我们可以看到，

二、常用的模型初始化方法