计数排序算法原理简介

前言

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

概念介绍

  • 计数排序算法是一个非基于比较的排序算法，故在排序的过程中不存在元素之间的比较和交换操作

  • 计数排序算法是一种以空间换取时间的做法，所以在一定范围内的整数排序时，它是快于任何比较排序算法

原理讲解

我们以[1 7 8 7 9 8 10 4]这个序列为例说明计数排序算法的实现原理

  1. 当未开始排序时，效果如下图

    在这里插入图片描述

  2. 先找到待排序序列中最大值10和最小值1，此时效果如下图

    在这里插入图片描述

  3. 新建一个长度为N=最大值10-最小值1+1=10的数组，新数组中值中值均为0，此时效果如下图

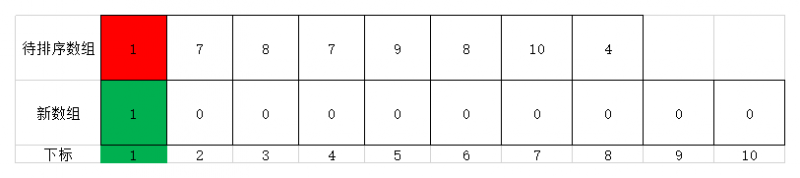
    在这里插入图片描述

  4. 开始遍历待排序的序列，第一个元素为1，故将值为1的元素放到新数组位置为1的地方，其值为元素1在原序列中出现的次数1次。此时效果如下图

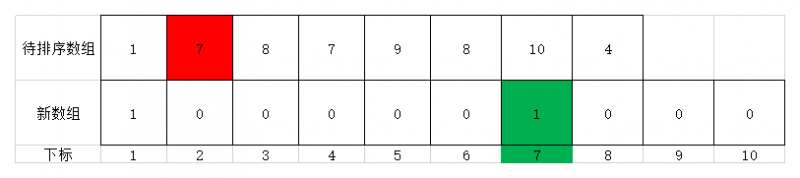
    在这里插入图片描述

  5. 继续遍历，第二个元素为7，故将值为7的元素放到新数组位置为7的地方，其值为元素7在原序列中出现的次数1次。此时效果如下图

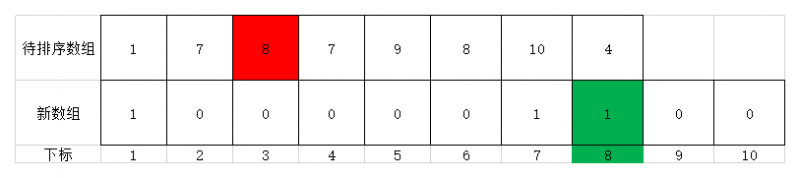
    在这里插入图片描述

  6. 继续遍历，第三个元素为8，故将值为8的元素放到新数组位置为8的地方，其值为元素8在原序列中出现的次数1次。此时效果如下图

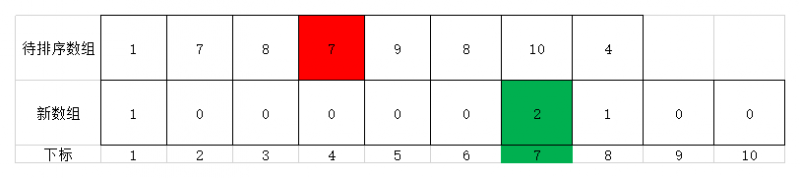
    在这里插入图片描述

  7. 继续遍历，第四个元素为7，故将值为7的元素放到新数组位置为7的地方，其值为元素7在原序列中出现的次数第2次。此时效果如下图

    在这里插入图片描述

  8. 继续遍历，第五个元素为9，故将值为9的元素放到新数组位置为9的地方，其值为元素9在原序列中出现的次数1次。此时效果如下图

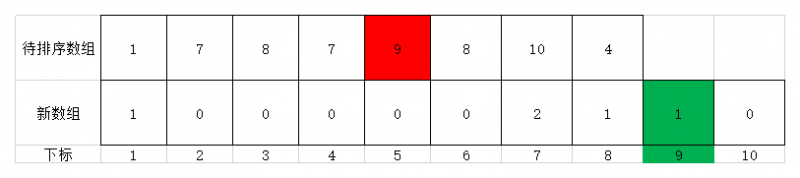
    在这里插入图片描述

  9. 继续遍历，第六个元素为8，故将值为8的元素放到新数组位置为8的地方，其值为元素8在原序列中出现的次数第2次。此时效果如下图

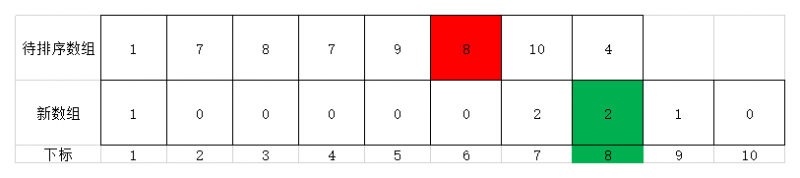
    在这里插入图片描述

  10. 继续遍历，第七个元素为10，故将值为10的元素放到新数组位置为10的地方，其值为元素10在原序列中出现的次数1次。此时效果如下图

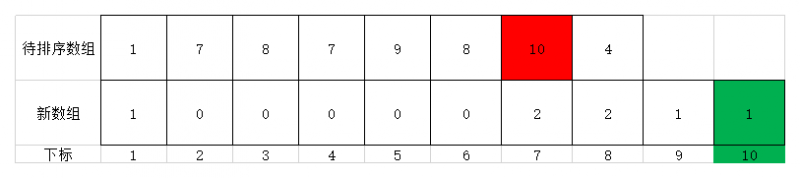
    在这里插入图片描述

  11. 继续遍历，第八个元素为4，故将值为4的元素放到新数组位置为4的地方，其值为元素4在原序列中出现的次数1次。此时效果如下图

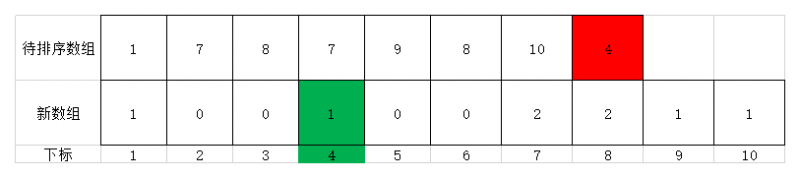
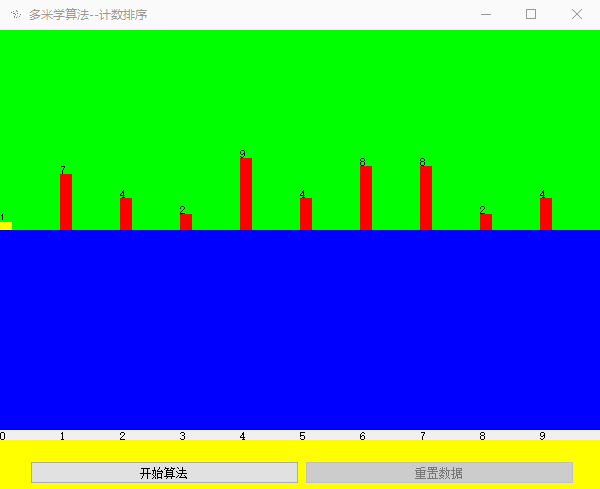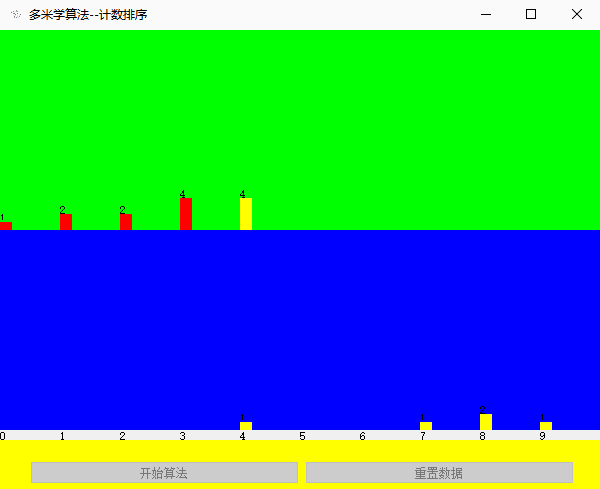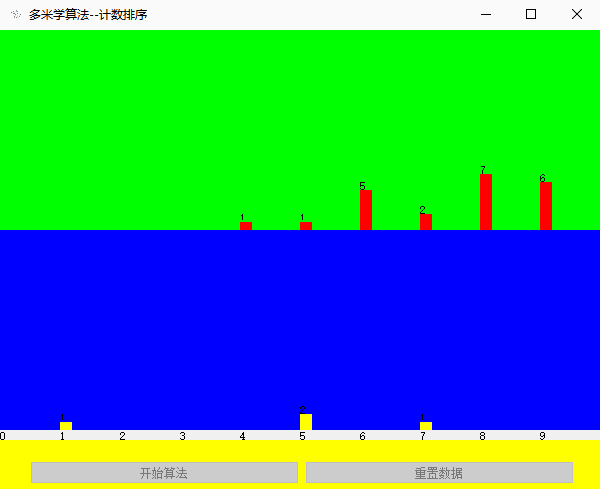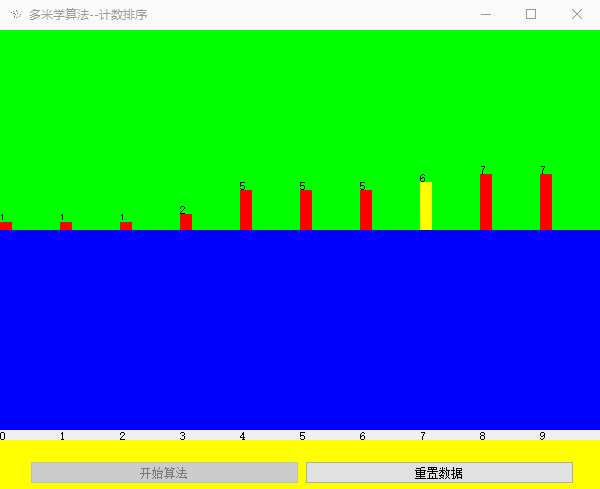
    在这里插入图片描述

  12. 至此，整个待排序数组遍历完毕，此时效果如下图

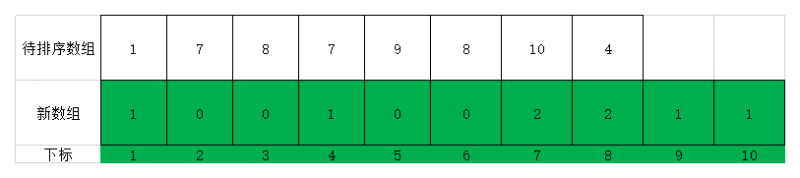
    在这里插入图片描述

    新数组中的每一个值，代表了其下标在待排序数组中出现的次数。

  13. 最后，我们遍历新数组，输出新数组元素的下标值，对应下标的值是几就输出几次。此时效果如下图

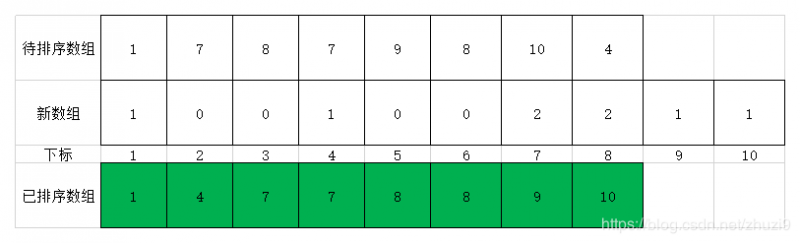
    在这里插入图片描述

时间复杂度

  • 计数排序的时间复杂度为O(n+k)。其中n为待排序元素个数，k为待排序元素最大值

空间复杂度

  • 计数排序的空间复杂度为n+O(k)。其中n为待排序元素个数，k为待排序元素最大值

算法优缺点

  • 优点：速度快

  • 缺点：

    • 需要提前知道待排序元素最大值

    • 需要大量内存消耗

效果展示

在这里插入图片描述

以上是 计数排序算法原理简介 的全部内容， 来源链接： utcz.com/a/25014.html

回到顶部