插入排序算法应该怎么插入?
前言
概念介绍
- 取出数组中无序部分的第一个元素,从后向前检查数组有序部分元素,将其插入到一个适当位置,使数组有序部分依然有序。当无序部分最后一个元素放入合适位置时,该数组排序完毕。
原理讲解
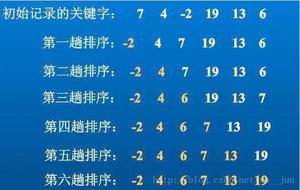
- 以41 34 19 17 2这个序列为例说明插入排序的实现原理
- 未开始遍历时,此时效果如下图
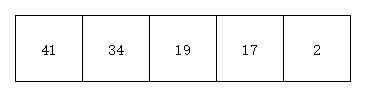
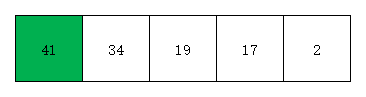
- 第一次遍历时,我们取出第一个元素41,并假定该元素已经有序。此时有序部分元素为41,无序部分元素为34 19 17 2。效果如下图
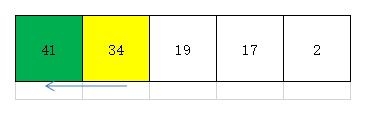
- 第二次遍历时,我们取出无序部分第一个元素34,检查有序部分元素41。效果如下图
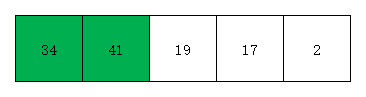
此时34小于41,故将元素34插到元素41的前面。此时有序部分元素为34 41,无序部分元素为19 17 2。效果如下图
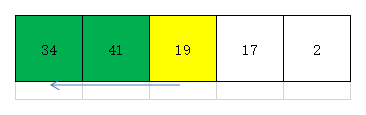
- 第三次遍历时,我们取出无序部分第一个元素19,检查有序部分元素34 41。效果如下图
此时19小于41,也小于34,故将元素19插到元素34的前面。此时有序部分元素为19 34 41,无序部分元素为17 2。效果如下图
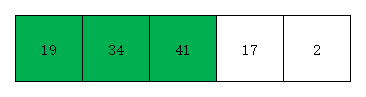
- 第四次遍历时,我们取出无序部分第一个元素17,检查有序部分元素19 34 41。效果如下图
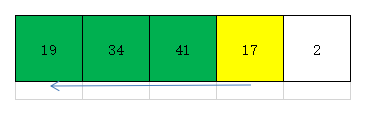
此时17小于41,小于34,也小于19,故将元素17插到元素19的前面。此时有序部分元素为17 19 34 41,无序部分元素为2。效果如下图
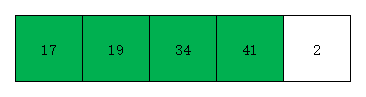
- 第五次遍历时,我们取出无序部分第一个元素2,检查有序部分元素17 19 34 41,效果如下图
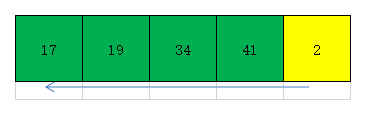
此时2小于41,小于34,小于19,也小于17,故将元素2插到元素17的前面。此时有序部分元素为2 17 19 34 41,无序部分元素为空。效果如下图
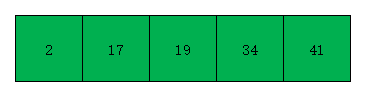
- 此时整个数组插入排序完毕。
时间复杂度
- 插入排序算法的时间复杂度是和算法中相邻两个数据的比较次数和移动次数成正比的。具体如下:
| 数据个数 | 最大比较次数 | 最大移动次数 |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 1 | 1 |
| 3 | 3 | 3 |
| 4 | 6 | 6 |
| 5 | 10 | 10 |
| 10 | 45 | 45 |
| N | 1/2N(N-1) | 1/2N(N-1) |
所以根据时间复杂度的概念,冒泡算法的时间复杂度为O(N^2)
空间复杂度
- 是对一个算法在运行过程中临时占用存储空间大小的度量。
- 由于插入排序算法前后占用空间大小不变,由空间复杂度含义可知,该算法空间复杂度为O(1)
算法优缺点
- 优点:稳定,快速
- 缺点:比较次数不一定,比较次数越少,插入点后的数据移动越多,特别是当数据总量庞大的时候
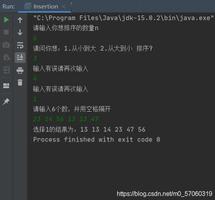
效果展示
源码下载
- 请在公众号中回复“算法源码”即可获得十大经典排序算法源码
更多算法学习请关注我的公众号

以上是 插入排序算法应该怎么插入? 的全部内容, 来源链接: utcz.com/a/24402.html