快排与堆排
快速排序
荷兰国旗问题(Dutch National Flag Problem)
给定一个数组arr,和一个数num;请把小于等于num的数放在数组的左边,大于num的数放在数组的右边。
要求额外空间复杂度O(1),时间复杂度O(N)
思路:
给定一个无序数组[4,5,6,7,2,1,9,8],num为5
使用一个变量p来划分小于等于num的范围,刚开始p=-1表示这个范围不存在。
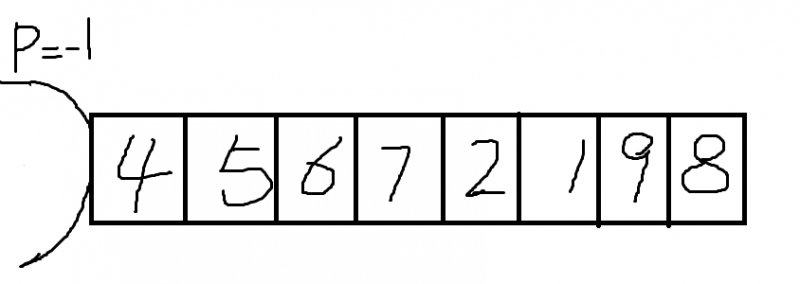
遍历数组,当出现小于等于num的数后,当前遍历到的数字与p的下一个数字发生交换,p加1

本示例中遍历到数组的第一个数小于num,所以当前数字和p的下一个位置的数,即自己交换。后续过程省略,代码如下:
public class Patition {public static void patition(int []arr,int num){
if(arr == null)
return;
int p = -1;
for(int i = 0;i<arr.length;i++){
if(arr[i]<=num)
swap(arr,i,++p);
}
return ;
}
public static void swap(int []arr,int i,int j){
if(arr == null || i == j)
return;
arr[i] = arr[i]^arr[j];
arr[j] = arr[i]^arr[j];
arr[i] = arr[i]^arr[j];
}
}
问题的升级:(荷兰国旗问题)Dutch National Flag Problem
给定一个整数数组,给定一个值K,这个值在原数组中一定存在;要求把数组中小于K的元素放到数组的左边,大于K的元素放到数组的右边,等于K的元素放到数组的中间;
最终返回一个整数数组,其中只有两个值,分别是等于K的数组部分的左右两个下标值。
例如:
给定数组:[2, 3, 1, 9, 7, 6, 1, 4, 5],给定一个值4,
那么经过处理原数组可能得一种情况是:[2, 3, 1, 1, 4, 9, 7, 6, 5].
需要注意的是,小于4的部分不需要有序,大于4的部分也不需要有序,返回等于4部分的左右两个下标,即[4, 4]
荷兰国旗问题较上问题增加了对等于区域划分的判断,在算法的思路上,我们可以再使用一个变量来跟踪大于num的区域:
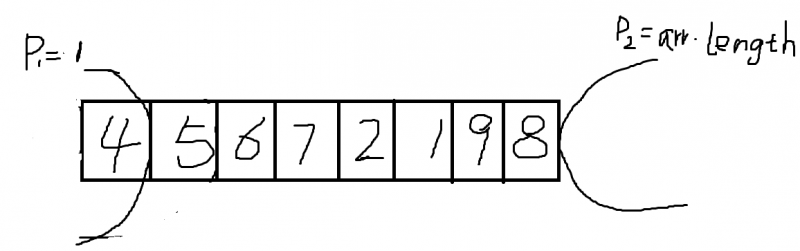
num为5,当遍历到5时,p1与p2不发生变化,小于与大于区域不发生扩张;遍历到大于num的数时,当前遍历的数与p2前的数发生交换,p2减1,表示大于num的数扩张了一个单位,并且遍历的索引停止:
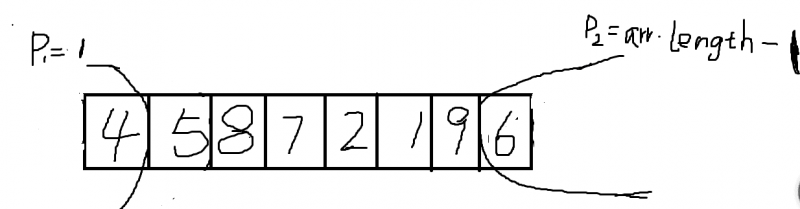
遍历到了数组的arr[2],发生交换后,继续判断arr[2]位置的数(8)与num的大小,直到当前遍历到的index与p2“相撞”后,停止。后续过程省略,代码如下:
public class DutchNationalFlag {public static int[] partition(int []arr,int L,int R,int num){
if(arr == null)
return null;
int p1 = L - 1;
int p2 = R + 1;
int curIndex = L;
while(curIndex < p2){
if(arr[curIndex] < num){
swap(arr,curIndex++,++p1);
}elseif(arr[curIndex] == num){
curIndex++;
}else{
swap(arr,curIndex,--p2);
}
}
return new int[]{++p1,--p2};
}
public static void swap(int[] arr,int i,int j){
if(arr == null || i == j)
return;
arr[i] = arr[i]^arr[j];
arr[j] = arr[i]^arr[j];
arr[i] = arr[i]^arr[j];
}
}
经典快排与改进
经典快排
经典快排的思路即:partition+recursion
partition选择数组的最后一个数为参考值,将小于等于该数字的数罗列到左边,该数字放在中间,大于这个数的数罗列到该数字的右边,然后对该数字左边的数和右边的数进行递归,完成排序。经典快排以及测试代码如下:
import java.util.Arrays;public class ClassicQuickSort {
public static void quickSort(int [] arr){
sort(arr,0,arr.length-1);
}
public static void sort(int []arr,int L,int R){
if(L < R){
int mid = partition(arr,L,R);
sort(arr,L,mid-1);
sort(arr,mid+1,R);
}
}
public static int partition(int []arr,int L,int R){
int p = L-1;
for(int i = L;i<R+1;i++){
if(arr[i]<=arr[R])
swap(arr,i,++p);
}
return p;
}
public static void swap(int []arr,int i,int j){
if(arr == null || i == j)
return;
arr[i] = arr[i]^arr[j];
arr[j] = arr[i]^arr[j];
arr[i] = arr[i]^arr[j];
}
// test:comparator
public static void comparator(int []arr){
Arrays.sort(arr);
}
// test :printer
public static void printArray(int[]arr){
if(arr == null)
return;
for(int i = 0;i<arr.length;i++){
System.out.print(arr[i]+ " ");
}
System.out.println();
}
// test: copier
public static int[] copier(int []arr){
if(arr == null)
return null;
int [] copyArr = new int[arr.length];
for(int i = 0;i<arr.length;i++){
copyArr[i] = arr[i];
}
return copyArr;
}
// test: generateRandomArray
public static int[] generateRandomArray(int maxSize,int maxValue){
int size = (int)((maxSize+1)*Math.random());
int[] arr = new int[size];
for(int i = 0;i<size;i++){
// (-maxValue,maxValue)
arr[i] = (int)((maxValue+1)*(Math.random()) - maxValue*Math.random());
}
return arr;
}
// test: isEqual
public static boolean isEqual(int[] arr1, int[] arr2){
if(arr1 != null&& arr2 == null || arr2 != null && arr1 == null)
returnfalse;
if(arr1.length != arr2.length)
returnfalse;
if(arr1 == null && arr2 == null)
returntrue;
for(int i = 0;i<arr1.length;i++){
if(arr1[i] != arr2[i])
returnfalse;
}
returntrue;
}
public static void main(String[]args){
int testTime = 5000;
int maxSize = 100;
int maxValue = 100;
boolean succeed = true;
for(int i = 0;i<testTime;i++){
int [] arr1 = generateRandomArray(maxSize,maxValue);
int [] arr2 = copier(arr1);
quickSort(arr1);
comparator(arr2);
if(!isEqual(arr1,arr2)){
succeed = false;
printArray(arr1);
printArray(arr2);
break;
}
}
System.out.println(succeed?"Nice":"Wrong");
}
}
改进快排
经典快排的问题是,每次只能排出一个数字,partition过程中是将num这个数字与小于等于区域和大于区域进行划分,如果有多个和num相等的数字,那么排序效率会变得十分低,由荷兰国旗问题的思考总结,我们可以进一步将快排进行优化改进。将partition过程变为将数组划分为小于区域,等于区域以及大于区域,然后对小于区域和大于区域再进行partition的递归。代码如下,省略测试代码:
public class QuickSort {public static void quickSort(int[] arr){
sort(arr,0,arr.length-1);
}
public static void sort(int[] arr,int L,int R){
if(L < R){
int [] indexArr = partition(arr,L,R);
sort(arr,L,indexArr[0]-1);
sort(arr,indexArr[1]+1,R);
}
}
public static int[] partition(int[] arr,int L,int R){
int p1 = L - 1;
int p2 = R ;
int curIndex = L;
while(curIndex < p2){
if(arr[curIndex] < arr[R]){
swap(arr,curIndex++,++p1);
}elseif(arr[curIndex] > arr[R]){
swap(arr,curIndex,--p2);
}else{
curIndex++;
}
}
swap(arr,p2,R);
return new int[]{++p1,--p2};
}
public static void swap(int[] arr,int i,int j){
if(arr == null || i == j)
return;
arr[i] = arr[i]^arr[j];
arr[j] = arr[i]^arr[j];
arr[i] = arr[i]^arr[j];
}
}
快排时间复杂度与额外空间复杂度分析
快排的时间复杂度与数据状况有关,一个有序的数组[0,1,2,3,4,5,6,7],如果使用快排排序,那么状况就是最差的。但是如果每次参考的基准数都能把数组均分成两部分那么我们就可以按照master公式来计算时间复杂度:T(N) = a*T(N/b) + O(N^d).快排分为两个子过程递归,除去递归外partition的时间复杂度为O(N),所以其时间复杂度为O(N^d * logN)即:O(NlogN)。但是如何使基准数能够将数组均分成两坨呢?为了解决这个问题,我们可以打乱当前的数据状况,sort部分的代码改动如下:
public static void sort(int[] arr,int L,int R){if(L < R){
swap(arr,L+(int)((R-L+1)*Math.random()),R);// 随机让任意位置的数与基准数位置R的数调换
int [] indexArr = partition(arr,L,R);
sort(arr,L,indexArr[0]-1);
sort(arr,indexArr[1]+1,R);
}
}
通过添加一句代码,就可以让未知状况的数组取基准数,转换成一个概率问题,通过长期数学期望最终计算得到随即快速排序的时间复杂度为O(NlogN)。
随机快速排序的额外空间复杂度为O(logN),原因在于,partition最后要返回一个数组来记录与基准数相等的区域索引范围,这样的额外数组量为一个二叉树的高度即logN。
堆排序
最大堆与最小堆
满二叉树
什么是满二叉树?国内定义如果一个二叉树的层数为K,且节点的总数是2^K-1,那么这棵树就是一个满二叉树,示例:
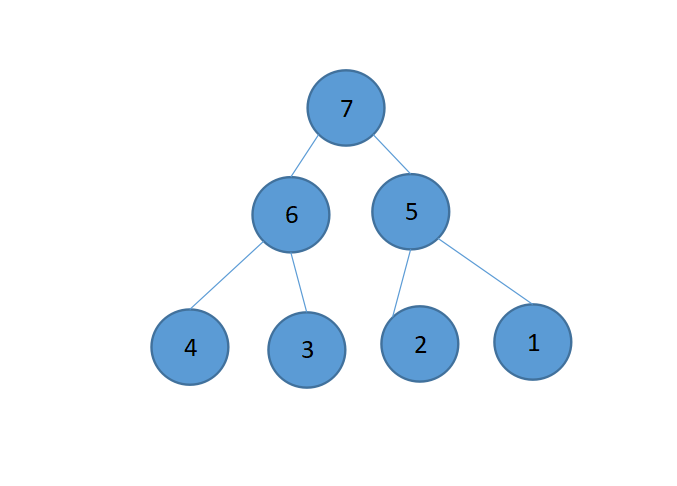
完全二叉树
节点从左至右依次排布的树就是完全二叉树,示例:
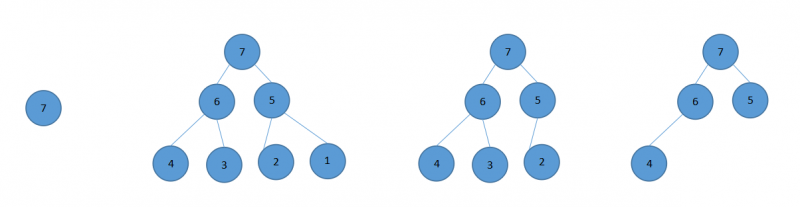
堆
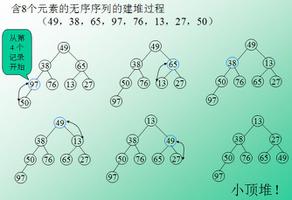
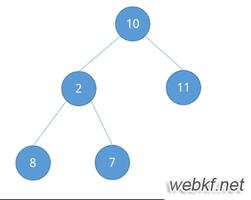
堆是一种完全二叉树,分为最大堆(大根堆)和最小堆(小根堆)。当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆,反之,当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。示例:
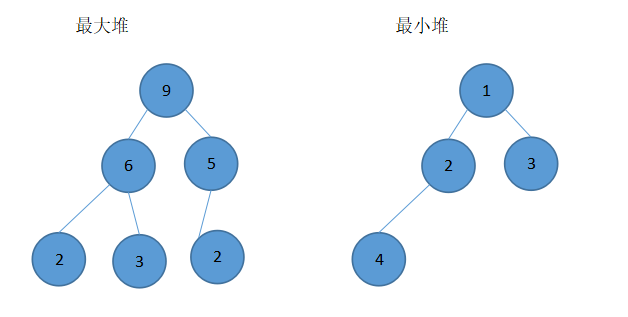
最大堆或最小堆的子树仍然是最大堆或最小堆。
heapInsert与heapify
heapInsert 与 heapify是堆结构中重要的两个方法。
heapInsert
heapInsert顾名思义,是向堆中插入节点,插入节点后,要判断该节点与其父节点的大小,如果大于父节点,那么则插入的节点与父节点交换位置,并继续向上判断,直到小于等于父节点为止。一个节点的父节点的索引为(index-1)/2。
public static void heapInsert(int[] arr,int index){while(arr[index] > arr[(index-1)/2]){
swap(arr,index,(index-1)/2);
index = (index-1)/2;
}
}
public static void swap(int[] arr,int i,int j){
if(arr == null || i == j)
return;
arr[i] = arr[i]^arr[j];
arr[j] = arr[i]^arr[j];
arr[i] = arr[i]^arr[j];
}
heapify
heapify的作用举例:
假设有一个流,它源源不断向外吐出数字,这些数字是没有规律的;现在希望你设计一种数据结构,可以快速地收集并获取吐出所有数字的中位数
如果你用一个数组去接收流吐出的数字,那么收集流吐出的数字很简单,但是如果要获取中位数的话就要对数组进行一次排序,如果要求流每次吐出一个数字就获取一次中位数,那么就要频繁地对数组进行排序操作。解决的方法就是使用堆结构来解决这个问题:设计一个最大堆,和一个最小堆,每次流吐出数字的时候都和最大堆的堆顶作比较,如果小于等于最大堆堆顶就放入最大堆,如果大于最大堆的堆顶则放入最小堆,入堆这个操作就是heapInsert。同时我们还需要保证最大堆的数据量不能比最小堆中的数据量大超过1,反之亦是如此/也就是要保持最大堆数据量N和最小堆的数据量M的关系为 |N-M| <= 1,如何保持这种关系呢?一旦破坏了这种关系的平衡,我们就让最大堆的顶部或者最小堆的顶部弹出,让这个最大的数字进入到最小堆里面,或者是让最小堆的最小的数字insert到最大堆里面,如图示意:
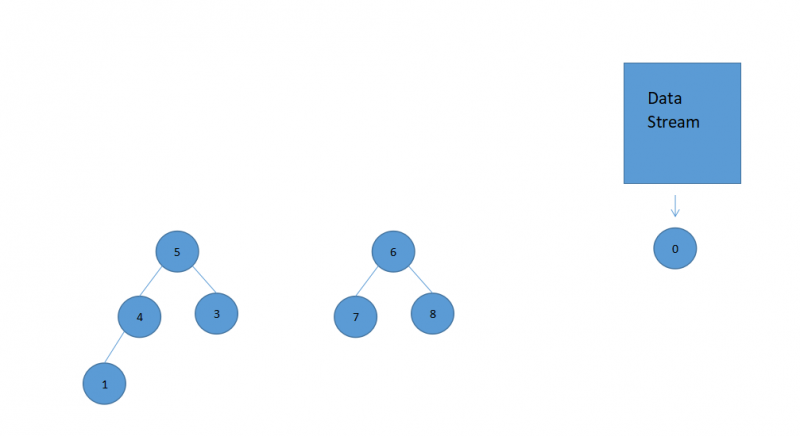
假设这个数据流吐出的数字依次是 5->6->4->7->3->8->1
左侧为最大堆数字数量为N,右侧为最小堆数字数量为M,没有破坏过 |N-M| <= 1的规定,如果这个时候数据流吐出的数字为0,那么就要heapInsert到最大堆里面,这个时候N-M = 2破坏了两堆数量上的平衡,所以要把最大堆的堆顶弹入到最小堆中去,操作如下:
首先将数字0 heapInsert到最大堆中
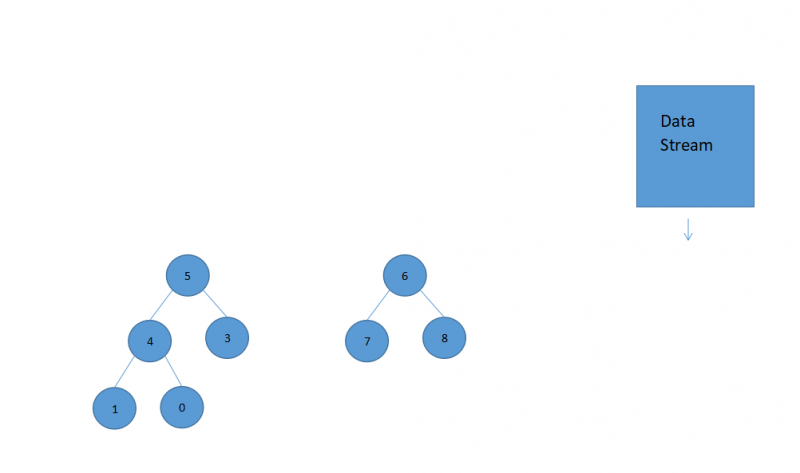
交换最大堆首尾数字
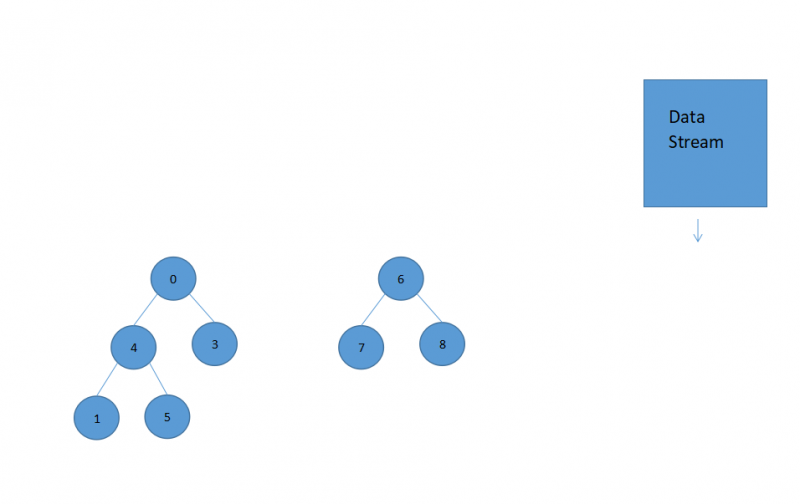
将最大堆末尾数字(5) heapInsert到最小堆
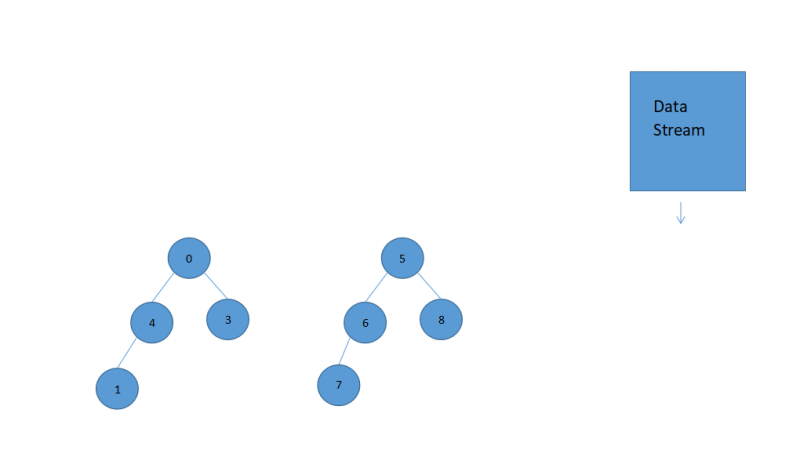
接下来就是heapify操作了,对最大堆中的堆顶0进行heapify,首先要判断它的两个孩子谁更大,谁大跟谁交换,直到满足最大堆的结构为止
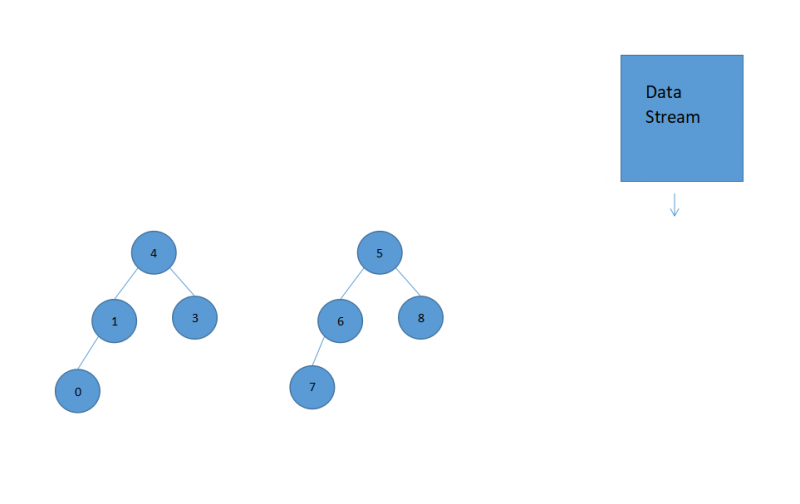
heapify的代码如下:
public static void heapify(int[] arr,int heapSize,int index){int leftIndex = 2*index+1;
while(leftIndex < heapSize){
int largestIndex = leftIndex+1<heapSize && arr[leftIndex]<arr[leftIndex+1]?leftIndex+1:leftIndex;
largestIndex = arr[index]>arr[largestIndex]?index:largestIndex;
if(largestIndex != index){
swap(arr,index,largestIndex);
index = largestIndex;
leftIndex = largestIndex*2+1;
}else {
break;
}
}
}
arr代表最大堆的数据,heapSize为最大堆数字的个数,index代表对哪个索引的数字进行heapify
堆排序
堆排序的思路就是对数组中的每个数字进行heapInsert操作,然后置换堆顶和堆末的数字,交换之后,最大的数字就排序好了,这时heapSize-1,然后对heapSize-1的这个堆的堆顶进行heapify,heapify操作后,这个heapSize-1的堆再次变为最大堆,然后再置换堆顶和堆末的数字,排出最大数字......代码如下:
public class HeapSort {public static void heapSort(int[] arr){
// 形成最大堆
for(int i = 0;i<arr.length;i++){
heapInsert(arr,i);
}
int heapSize = arr.length;
while(heapSize > 0){
swap(arr,0,heapSize-1);
heapSize--;
heapify(arr,heapSize,0);
}
}
public static void swap(int[] arr,int i,int j){
if(arr == null || i == j)
return;
arr[i] = arr[i]^arr[j];
arr[j] = arr[i]^arr[j];
arr[i] = arr[i]^arr[j];
}
public static void heapInsert(int[] arr,int index){
while(arr[index] > arr[(index-1)/2]){
swap(arr,index,(index-1)/2);
index = (index-1)/2;
}
}
public static void heapify(int[] arr,int heapSize,int index){
int leftIndex = 2*index+1;
while(leftIndex < heapSize){
int largestIndex = leftIndex+1<heapSize && arr[leftIndex]<arr[leftIndex+1]?leftIndex+1:leftIndex;
largestIndex = arr[index]>arr[largestIndex]?index:largestIndex;
if(largestIndex != index){
swap(arr,index,largestIndex);
index = largestIndex;
leftIndex = largestIndex*2+1;
}else {
break;
}
}
}
}
堆排序heapInsert花费的时间为log1+log2+log3+log4...+logN;heapify的操作也是相当于每个元素依次遍历二叉树的高度,因为有O(log1+log2+...+logn)=O(log(n!))=O(nlogn)所以堆排序的时间复杂度为O(NlogN),且堆排序的额外空间复杂度为O(1)。
以上是 快排与堆排 的全部内容, 来源链接: utcz.com/a/21334.html