数据结构:队列之循环队列
原理分析
结构" title="数据结构">数据结构
FIFO:先进先出
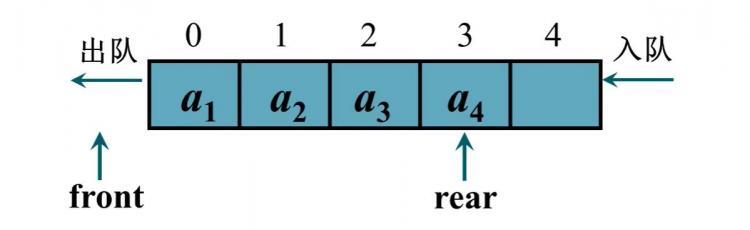
front指向头元素的前一个位置
rear指向最后一个元素
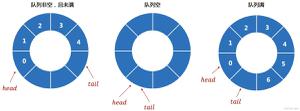
如果用rear=front来判断队列为空还是满,会出现歧义,其实无法判断
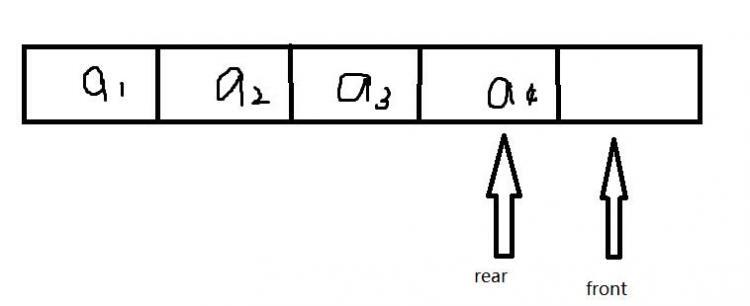
此时,若再插入一个元素,则rear=front。
为了解决这个问题,本问采取留出一个空间不用的策略。及队列容量始终比开辟空间少一。
基本数据类型
class CirQueue {private:
T* data;
int front;
int rear;
int mSize;
public:
CirQueue();
CirQueue(int size);
~CirQueue();
bool enQueue(T item); //入队
bool deQueue(T &item); //出队
bool getFront(T& item);//获得队头
bool isEmpty();
bool isFull();
void clearQueue();
void displayQueue();
int queueLength(); //获得队列长度
class Out_of_range{}; //异常类
class Empty{}; //异常类
};
队列初始化
template<class T>CirQueue<T>::CirQueue()
{
front = rear = 0;
mSize = QUEUESIZE;
data = new T[mSize];
}
template<class T>CirQueue<T>::CirQueue(int size)
{
mSize = size;
front = rear = 0;
data = new T[mSize];
}
析构函数
CirQueue<T>::~CirQueue(){
delete[] data;
}
入队(尾入)
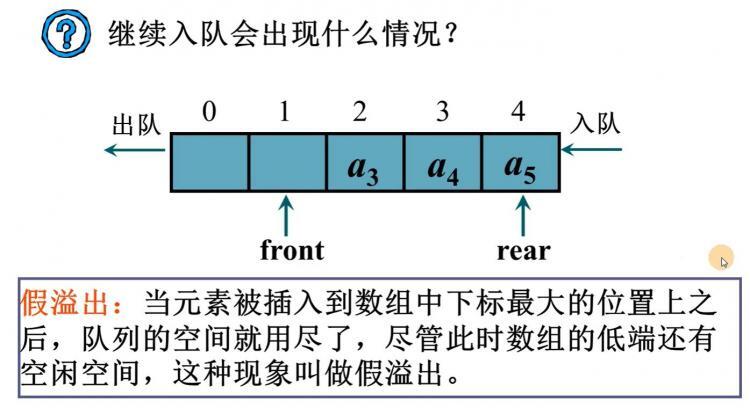
而使用循环队列可以解决此问题,充分利用空间。
bool CirQueue<T>::enQueue(T item){
if (isFull()) throw Out_of_range();
rear = (rear + 1) % mSize; //实现循环队列
data[rear] = item;
return true;
}
出队(头出)
template<class T>bool CirQueue<T>::deQueue(T& item)
{
if (isEmpty()) throw Empty();
front = (front + 1) % mSize;
item = data[front];
return true;
}
获取头元素
template<class T>bool CirQueue<T>::getFront(T& item)
{
if (isEmpty()) throw Empty();
int i = (front + 1) % mSize;
item = data[i];
return true;
}
判断是否为空
rear = front时为空
template<class T>bool CirQueue<T>::isEmpty()
{
if (rear ==front) return true;
return false;
}
判断是否为满
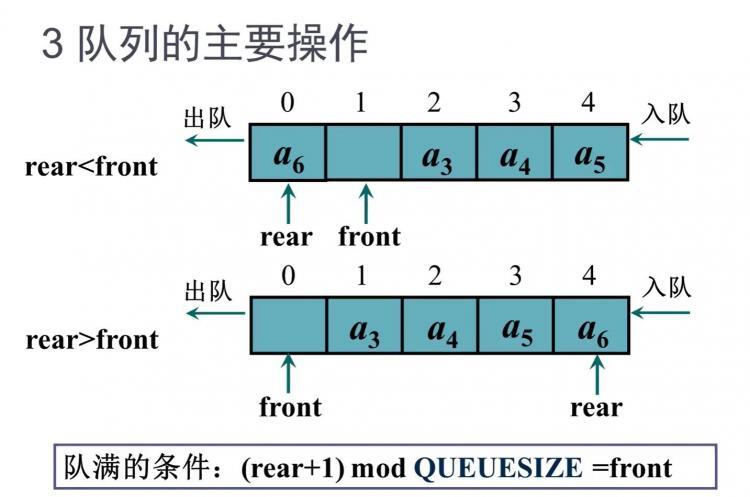
template<class T>bool CirQueue<T>::isFull()
{
if ((rear + 1) % mSize == front) return true;
return false;
}
清空队列
void CirQueue<T>::clearQueue(){
front = rear = 0;
}
打印队列
template<class T>void CirQueue<T>::displayQueue()
{
if (isEmpty()) {
cout << "队列为空" << endl;
return;
}
int i = (front + 1) % mSize;
while (1) { //当front=head时表示下标到达最后一个元素,打印完这个元素以后再退出
cout << data[i] << " ";
if (i == rear) break;
i = (i + 1) % mSize;
}
cout << endl;
}
获取队列长度
template<class T>int CirQueue<T>::queueLength()
{
int length = (rear + mSize - front) % mSize;
return length;
}
完整代码
#include<iostream>using namespace std;
const int QUEUESIZE = 100;
template <class T>
class CirQueue {
private:
T* data;
int front;
int rear;
int mSize;
public:
CirQueue();
CirQueue(int size);
~CirQueue();
bool enQueue(T item);
bool deQueue(T &item);
bool getFront(T& item);
bool isEmpty();
bool isFull();
void clearQueue();
void displayQueue();
int queueLength();
class Out_of_range{};
class Empty{};
};
template<class T>
CirQueue<T>::CirQueue()
{
front = rear = 0;
mSize = QUEUESIZE;
data = new T[mSize];
}
template<class T>
CirQueue<T>::CirQueue(int size)
{
mSize = size;
front = rear = 0;
data = new T[mSize];
}
template<class T>
CirQueue<T>::~CirQueue()
{
delete[] data;
}
template<class T>
bool CirQueue<T>::enQueue(T item)
{
if (isFull()) throw Out_of_range();
rear = (rear + 1) % mSize;
data[rear] = item;
return true;
}
template<class T>
bool CirQueue<T>::deQueue(T& item)
{
if (isEmpty()) throw Empty();
front = (front + 1) % mSize;
item = data[front];
return true;
}
template<class T>
bool CirQueue<T>::getFront(T& item)
{
if (isEmpty()) throw Empty();
int i = (front + 1) % mSize;
item = data[i];
return true;
}
template<class T>
bool CirQueue<T>::isEmpty()
{
if (rear ==front) return true;
return false;
}
template<class T>
bool CirQueue<T>::isFull()
{
if ((rear + 1) % mSize == front) return true;
return false;
}
template<class T>
void CirQueue<T>::clearQueue()
{
front = rear = 0;
}
template<class T>
void CirQueue<T>::displayQueue()
{
if (isEmpty()) {
cout << "队列为空" << endl;
return;
}
int i = (front + 1) % mSize;
while (1) {
cout << data[i] << " ";
if (i == rear) break;
i = (i + 1) % mSize;
}
cout << endl;
}
template<class T>
int CirQueue<T>::queueLength()
{
int length = (rear + mSize - front) % mSize;
return length;
}
int main(){
try {
CirQueue<int> Queue(3);
/*Queue.enQueue(1);
Queue.enQueue(2);*/
//int de ;
//Queue.deQueue(de);
//cout << de << endl;
//Queue.displayQueue();
//if (Queue.isFull()) cout << "full";
//cout << Queue.queueLength();
//Queue.clearQueue();
Queue.displayQueue();
}
catch (CirQueue<int>::Out_of_range) {
cout << "已经满了" << endl;
}
catch (CirQueue<int>::Empty) {
cout << "为空" << endl;
}
return 0;
}
以上是 数据结构:队列之循环队列 的全部内容, 来源链接: utcz.com/a/122401.html