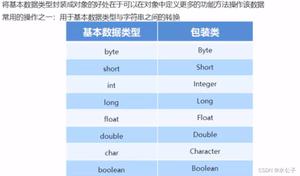
Java二叉树结构基础
package com.lin.tree_0308;public class ArrBinaryTreeDemo {
public static void main(String[] args) {
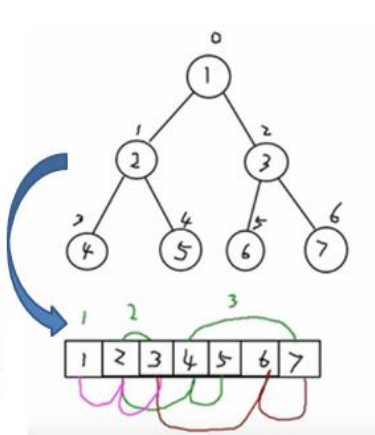
int[] arr = {1,2,3,4,5,6,7};
ArrBinaryTree arrBinaryTree = new ArrBinaryTree(arr);
System.out.println("前序遍历:");
arrBinaryTree.preOrder();
System.out.println();
System.out.println("中序遍历:");
arrBinaryTree.infixOrder();
System.out.println();
System.out.println("后序遍历:");
arrBinaryTree.postOrder();
}
}
class ArrBinaryTree{
private int[] arr;
public ArrBinaryTree(int[] arr) {
super();
this.arr = arr;
}
// 重载
public void preOrder() {
this.preOrder(0);
}
public void infixOrder() {
this.infixOrder(0);
}
public void postOrder() {
this.postOrder(0);
}
/**
*
* @Description:
* @author LinZM
* @date 2021-3-8 19:14:45
* @version V1.8
* @param index 数组下标
*/
// 前序遍历
public void preOrder(int index) {
if(arr == null || arr.length == 0) {
System.out.println("数组为空!");
}
// 输出当前数据
System.out.print(arr[index] + " ");
// 向左递归
if( ( index * 2 + 1 ) < arr.length ) {
preOrder( index * 2 + 1 );
}
// 向右递归
if( ( index * 2 +2 ) < arr.length ) {
preOrder( index * 2 + 2 );
}
}
// 中序遍历
public void infixOrder(int index) {
if(arr == null || arr.length == 0) {
System.out.println("数组为空!");
}
// 向左递归
if( ( index * 2 + 1 ) < arr.length) {
infixOrder( index * 2 + 1);
}
// 输出当前数据
System.out.print(arr[index] + " ");
// 向右递归
if( ( index * 2 + 2 ) < arr.length) {
infixOrder(index*2 + 2);
}
}
// 后序遍历
public void postOrder(int index) {
if(arr == null || arr.length == 0) {
System.out.println("数组为空!");
}
// 向左递归
if( ( index * 2 + 1) < arr.length ) {
postOrder(index * 2 + 1);
}
// 向右递归
if( ( index * 2 + 2 ) < arr.length) {
postOrder(index * 2 + 2);
}
// 输出当前数据
System.out.print(arr[index] + " ");
}
}

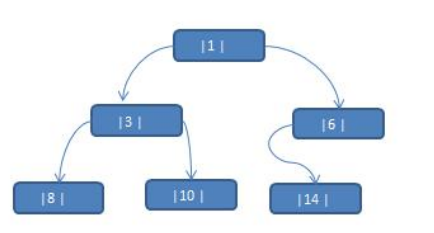
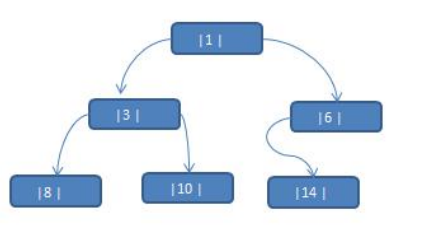
package com.lin.tree_0308;public class ThreadeBinaryTreeDemo {
public static void main(String[] args) {
TNode tNode1 = new TNode(1, "Tom");
TNode tNode2 = new TNode(3, "Jack");
TNode tNode3 = new TNode(6, "Smith");
TNode tNode4 = new TNode(8, "Marry");
TNode tNode5 = new TNode(10, "Linda");
TNode tNode6 = new TNode(14, "King");
tNode1.setLeft(tNode2);
tNode1.setRight(tNode3);
tNode2.setLeft(tNode4);
tNode2.setRight(tNode5);
tNode3.setLeft(tNode6);
TBinaryTree tBinaryTree = new TBinaryTree();
tBinaryTree.setRoot(tNode1);
tBinaryTree.threadedInfixNodes(tNode1);// 10test
TNode left = tNode5.getLeft();
TNode right = tNode5.getRight();
System.out.println(left);
System.out.println(right);
// // 中序遍历线索化二叉树
// System.out.println("中序遍历线索化二叉树:");
// tBinaryTree.threadedInfixList();
}
}
class TBinaryTree{
private TNode root;
// 前驱节点的指针,总是保留前一个节点
private TNode pre;
public void setRoot(TNode root) {
this.root = root;
}
public void threadedPreNodes(TNode node) {
if(node == null) {
System.out.println("空!!!");
return;
}
// 1 线索当前节点
// 先处理节点的前驱节点
if (node.getLeft() == null) {
// 让当前节点的左指针指向前驱节点
node.setLeft(pre);
// 修改当前节点的左指针的类型
node.setLeftType(1);
}
// 处理后继节点
if (pre != null && pre.getRight() == null) {
pre.setRight(node);
pre.setRigthType(1);
}
// 每处理一个节点后,让当前节点是下一个节点前驱节点
pre = node;
threadedPreNodes(node.getLeft());
threadedPreNodes(node.getRight());
}
// 二叉树中序线索化
/**
*
* @Description:
* @author LinZM
* @date 2021-3-8 22:14:51
* @version V1.8
* @param node 线索化节点
*/
public void threadedInfixNodes(TNode node) {
if(node == null) {
return;
}
// 1 先线索化左子树
threadedInfixNodes(node.getLeft());
// 2 线索化当前节点
// 先处理节点的前驱节点
// 节点8->节点3,一开始8为node,后面3为node
if(node.getLeft() == null ) {
// 让当前节点的左指针指向前驱节点
node.setLeft(pre);
// 修改当前节点的左指针的类型
node.setLeftType(1);
}
// 处理后继节点
if(pre != null && pre.getRight() == null) {
pre.setRight(node);
pre.setRigthType(1);
}
// 每处理一个节点后,让当前节点是下一个节点前驱节点
// pre = 8
pre = node;
// 3 线索化右子树
threadedInfixNodes(node.getRight());
}
// 中序遍历线索二叉树
public void threadedInfixList() {
// 定义一个变量,存储当前遍历的节点,从root开始
TNode node = root;
if(node == null) {
System.out.println("空树!");
return;
}
while(node != null) {
// 循环找到leftType == 1 的节点,第一个找到就是8节点
// 后面随着遍历而变化,因为当leftType == 1,说明该节点是按照线索化处理后的有效节点
while(node.getLeftType() == 0) {
node = node.getLeft();
}
// 找到8节点
System.out.println(node);
// 如果当前节点的右指针指向的是后继节点,就一直输出
while(node.getRigthType() == 1) {
node = node.getRight();
System.out.println(node);
}
// 如果不是后继节点,则替换这个遍历的节点
node = node.getRight();
}
}
// 删除节点
public void delNode(int no) {
if (root != null) {
// 如果只有一个root
if (root.getNo() == no) {
root = null;
} else {
root.delNode(no);
}
} else {
System.out.println("空树!");
}
}
// 前序遍历
public void preOrder() {
if(this.root != null) {
this.root.preOrder();
} else {
System.out.println("二叉树为空!");
}
}
// 中序遍历
public void infixOrder() {
if(this.root != null) {
this.root.infixOrder();
} else {
System.out.println("二叉树为空!");
}
}
// 后序遍历
public void postOrder() {
if(this.root != null) {
this.root.postOrder();
} else {
System.out.println("二叉树为空!");
}
}
// 前序查找
public TNode preOrderSearch(int no) {
if(root != null) {
return root.preOrderSearch(no);
} else {
return null;
}
}
// 中序查找
public TNode infixOrderSearch(int no) {
if (root != null) {
return root.infixOrderSearch(no);
} else {
return null;
}
}
// 后序查找
public TNode postOrderSearch(int no) {
if (root != null) {
return root.postOrderSearch(no);
} else {
return null;
}
}
}
class TNode{
private String name;
private int no;
private TNode left;
private TNode right;
// leftType == 0 为左子树, 如果为1则表示指向前驱节点
// rightType == 0 为右子树, 如果为1则表示指向后继节点
private int leftType;
private int rigthType;
public int getLeftType() {
return leftType;
}
public void setLeftType(int leftType) {
this.leftType = leftType;
}
public int getRigthType() {
return rigthType;
}
public void setRigthType(int rigthType) {
this.rigthType = rigthType;
}
public TNode(int no, String name) {
this.no = no;
this.name = name;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public TNode getLeft() {
return left;
}
public void setLeft(TNode left) {
this.left = left;
}
public TNode getRight() {
return right;
}
public void setRight(TNode right) {
this.right = right;
}
@Override
public String toString() {
return "TNode [name=" + name + ", no=" + no + "]";
}
// 前序遍历
public void preOrder() {
System.out.println(this); // 输出父节点
if(this.left != null) {
this.left.preOrder();
}
if(this.right != null) {
this.right.preOrder();
}
}
// 中序遍历
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this); // 输出父节点
if (this.right != null) {
this.right.infixOrder();
}
}
// 前序遍历
public void postOrder() {
if (this.left != null) {
this.left.postOrder();
}
if (this.right != null) {
this.right.postOrder();
}
System.out.println(this); // 输出父节点
}
// 前序查找
public TNode preOrderSearch(int no) {
System.out.println("1");
// 比较当前节点是不是
if(this.no == no) {
return this;
}
// 1 判断当前节点的左节点是否为空,如果不为空,则递归前序查找
// 2 如果左递归前序查找,找到节点,则返回
TNode resNode = null;
if(this.left != null) {
resNode = this.left.preOrderSearch(no);
}
if(resNode != null) {// 说明左子树找到了
return resNode;
}
// 1 左递归如果没有找到,则继续判断
// 2 当前节点的右节点是否为空,如果不为空,则继续向右递归前序查找
if(this.right != null) {
resNode = this.right.preOrderSearch(no);
}
// 这时候不管有没有找到都要返回resNode
return resNode;
}
// 中序查找
public TNode infixOrderSearch(int no) {
TNode resNode = null;
if(this.left != null) {
resNode = this.left.infixOrderSearch(no);
}
if(resNode != null) {
return resNode;
}
System.out.println("1");
if(this.no == no) {
return this;
}
if(this.right != null) {
resNode = this.right.infixOrderSearch(no);
}
return resNode;
}
// 后序查找
public TNode postOrderSearch(int no) {
TNode resNode = null;
if(this.left != null) {
resNode = this.left.postOrderSearch(no);
}
if(resNode != null) {
return resNode;
}
if(this.right != null) {
resNode = this.right.postOrderSearch(no);
}
if(resNode != null) {
return resNode;
}
System.out.println("1");
if(this.no == no) {
return this;
}
// 如果都没有找到
return resNode;
}
/**
*
* @Description:1 因为我们的二叉树是单向,所以我们是判断当前节点的子节点是否需要删除节点,而不是直接去判断当前节点是否需要删除节点。<br>
* 2 如果当前节点的左子节点不为空,并且左子节点就是要删除节点,就将this.left = null;并且就返回(结束递归删除) <br>
* 3 如果当前节点的右子节点不为空,并且右子节点就是要删除节点,就将this.right = null;并且就返回(结束递归删除) <br>
* 4 如果第2和第3都没有删除节点,那么我们就需要向左子树进行递归删除<br>
* 5 如果第4补也没有删除节点,则向右子树进行递归删除<br>
* @author LinZM
* @date 2021-3-8 15:17:32
* @version V1.8
*/
public void delNode(int no) {
if(this.left != null && this.left.no == no) {
this.left = null;
return;
}
if(this.right != null && this.right.no == no) {
this.right = null;
return;
}
if(this.left != null) {
this.left.delNode(no);
}
if(this.right != null) {
this.right.delNode(no);
}
}
}
仅供参考,有错误还请指出!
有什么想法,评论区留言,互相指教指教。
觉得不错的可以点一下右边的推荐哟
以上是 Java二叉树结构基础 的全部内容, 来源链接: utcz.com/a/121448.html