【算法】堆排序各语言版本实现

• Z时代
• 2024-01-10
• 分类：技术分享

堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法：

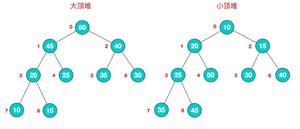
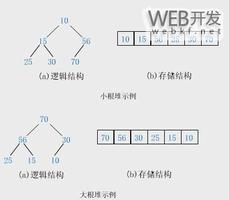
1. 大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列；
2. 小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列；

堆排序的平均时间复杂度为 Ο(nlogn)。

1. 创建一个堆 H[0……n-1]；
2. 把堆首（最大值）和堆尾互换；
3. 把堆的尺寸缩小 1，并调用 shift_down(0)，目的是把新的数组顶端数据调整到相应位置；
4. 重复步骤 2，直到堆的尺寸为 1。

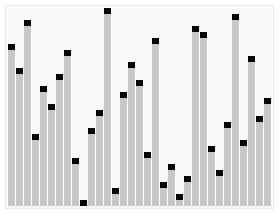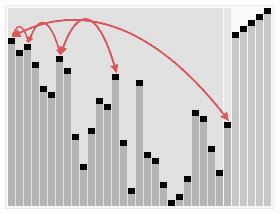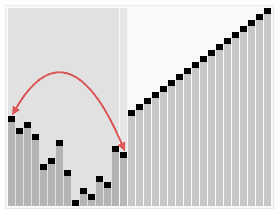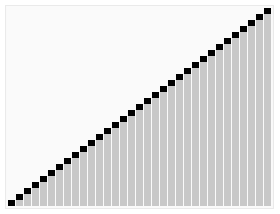
实例

var len;    // 因为声明的多个函数都需要数据长度，所以把len设置成为全局变量
function buildMaxHeap(arr) {   // 建立大顶堆
len = arr.length;
for (var i = Math.floor(len/2); i >= 0; i--) {
heapify(arr, i);
}
}
function heapify(arr, i) {     // 堆调整
var left = 2 * i + 1,
right = 2 * i + 2,
largest = i;
if (left  arr[largest]) {
largest = left;
}
if (right  arr[largest]) {
largest = right;
}
if (largest != i) {
swap(arr, i, largest);
heapify(arr, largest);
}
}
function swap(arr, i, j) {
var temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
function heapSort(arr) {
buildMaxHeap(arr);
for (var i = arr.length-1; i > 0; i--) {
swap(arr, 0, i);
len--;
heapify(arr, 0);
}
return arr;
}

实例

def buildMaxHeap(arr):
import math
for i in range(math.floor(len(arr)/2),-1,-1):
heapify(arr,i)
def heapify(arr, i):
left = 2*i+1
right = 2*i+2
largest = i
if left  arr[largest]:
largest = left
if right  arr[largest]:
largest = right
if largest != i:
swap(arr, i, largest)
heapify(arr, largest)
def swap(arr, i, j):
arr[i], arr[j] = arr[j], arr[i]
def heapSort(arr):
global arrLen
arrLen = len(arr)
buildMaxHeap(arr)
for i in range(len(arr)-1,0,-1):
swap(arr,0,i)
arrLen -=1
heapify(arr, 0)
return arr

实例

func heapSort(arr []int) []int {
arrLen := len(arr)
buildMaxHeap(arr, arrLen)
for i := arrLen - 1; i >= 0; i-- {
swap(arr, 0, i)
arrLen -= 1
heapify(arr, 0, arrLen)
}
return arr
}
func buildMaxHeap(arr []int, arrLen int) {
for i := arrLen / 2; i >= 0; i-- {
heapify(arr, i, arrLen)
}
}
func heapify(arr []int, i, arrLen int) {
left := 2*i + 1
right := 2*i + 2
largest := i
if left  arr[largest] {
largest = left
}
if right  arr[largest] {
largest = right
}
if largest != i {
swap(arr, i, largest)
heapify(arr, largest, arrLen)
}
}
func swap(arr []int, i, j int) {
arr[i], arr[j] = arr[j], arr[i]
}

实例

public class HeapSort implements IArraySort {
@Override
public int[] sort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝，不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
int len = arr.length;
buildMaxHeap(arr, len);
for (int i = len - 1; i > 0; i--) {
swap(arr, 0, i);
len--;
heapify(arr, 0, len);
}
return arr;
}
private void buildMaxHeap(int[] arr, int len) {
for (int i = (int) Math.floor(len / 2); i >= 0; i--) {
heapify(arr, i, len);
}
}
private void heapify(int[] arr, int i, int len) {
int left = 2 * i + 1;
int right = 2 * i + 2;
int largest = i;
if (left  arr[largest]) {
largest = left;
}
if (right  arr[largest]) {
largest = right;
}
if (largest != i) {
swap(arr, i, largest);
heapify(arr, largest, len);
}
}
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}

实例

function buildMaxHeap(&$arr)
{
global $len;
for ($i = floor($len/2); $i >= 0; $i--) {
heapify($arr, $i);
}
}
function heapify(&$arr, $i)
{
global $len;
$left = 2 * $i + 1;
$right = 2 * $i + 2;
$largest = $i;
if ($left  $arr[$largest]) {
$largest = $left;
}
if ($right  $arr[$largest]) {
$largest = $right;
}
if ($largest != $i) {
swap($arr, $i, $largest);
heapify($arr, $largest);
}
}
function swap(&$arr, $i, $j)
{
$temp = $arr[$i];
$arr[$i] = $arr[$j];
$arr[$j] = $temp;
}
function heapSort($arr) {
global $len;
$len = count($arr);
buildMaxHeap($arr);
for ($i = count($arr) - 1; $i > 0; $i--) {
swap($arr, 0, $i);
$len--;
heapify($arr, 0);
}
return $arr;
}

实例

#include 
#include 
void swap(int *a, int *b) {
int temp = *b;
*b = *a;
*a = temp;
}
void max_heapify(int arr[], int start, int end) {
// 建立父節點指標和子節點指標
int dad = start;
int son = dad * 2 + 1;
while (son  arr[son]) //如果父節點大於子節點代表調整完畢，直接跳出函數
return;
else { // 否則交換父子內容再繼續子節點和孫節點比較
swap(&arr[dad], &arr[son]);
dad = son;
son = dad * 2 + 1;
}
}
}
void heap_sort(int arr[], int len) {
int i;
// 初始化，i從最後一個父節點開始調整
for (i = len / 2 - 1; i >= 0; i--)
max_heapify(arr, i, len - 1);
// 先將第一個元素和已排好元素前一位做交換，再重新調整，直到排序完畢
for (i = len - 1; i > 0; i--) {
swap(&arr[0], &arr[i]);
max_heapify(arr, 0, i - 1);
}
}
int main() {
int arr[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
int len = (int) sizeof(arr) / sizeof(*arr);
heap_sort(arr, len);
int i;
for (i = 0; i

实例
#include 
#include 
using namespace std;
void max_heapify(int arr[], int start, int end) {
// 建立父節點指標和子節點指標
int dad = start;
int son = dad * 2 + 1;
while (son  arr[son]) // 如果父節點大於子節點代表調整完畢，直接跳出函數
return;
else { // 否則交換父子內容再繼續子節點和孫節點比較
swap(arr[dad], arr[son]);
dad = son;
son = dad * 2 + 1;
}
}
}
void heap_sort(int arr[], int len) {
// 初始化，i從最後一個父節點開始調整
for (int i = len / 2 - 1; i >= 0; i--)
max_heapify(arr, i, len - 1);
// 先將第一個元素和已经排好的元素前一位做交換，再從新調整(刚调整的元素之前的元素)，直到排序完畢
for (int i = len - 1; i > 0; i--) {
swap(arr[0], arr[i]);
max_heapify(arr, 0, i - 1);
}
}
int main() {
int arr[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
int len = (int) sizeof(arr) / sizeof(*arr);
heap_sort(arr, len);
for (int i = 0; i

以上是 【算法】堆排序各语言版本实现 的全部内容， 来源链接： utcz.com/a/120458.html